题目内容
10.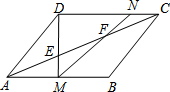 平行四边形ABCD中,AB=28,E、F是对角线AC上的两点,且AE=EF=FC,DE交AB于点M,MF交CD于点N.求AM、CN的长.
平行四边形ABCD中,AB=28,E、F是对角线AC上的两点,且AE=EF=FC,DE交AB于点M,MF交CD于点N.求AM、CN的长.
分析 根据已知条件,先证明△AEM∽△CED,然后利用相似三角形的对应边成比例这一性质求得AM=$\frac{1}{2}$AB;再来证明△AFM∽△CFN,依据相似三角形的性质求的CN的长度.
解答 解:在△AEM和△CED中,
∠CAB=∠DCA(内错角相等),
∠AEM=∠CED,
∴△AEM∽△CED,
∴$\frac{AM}{CD}=\frac{AE}{EC}$,
∵AE=EF=FC,
∴$\frac{AM}{CD}=\frac{AE}{EC}$=$\frac{1}{2}$,
∴AM=$\frac{1}{2}$CD;
∵AB=CD,
∴AM=$\frac{1}{2}$AB=14,①;
在△AFM和△CFN中,
∠FAM=∠FCN(内错角相等),∠AFM=∠CFN(对顶角相等),
∴△AFM∽△CFN,
∴$\frac{AM}{CN}=\frac{AF}{CF}$=2,
∴CN=$\frac{1}{2}$AM②;
∵AB=28 ③
由①②③解得,CN=7.
点评 本题主要考查了相似三角形的判定定理:两个三角形中,两个对应角相等,则这两个三角形相似,以及相似三角形的性质:对应边成比例.

练习册系列答案
相关题目
5.设a≠b,m≠n,a,b,m,n是已知数,则方程组$\left\{\begin{array}{l}\frac{x}{a+m}+\frac{y}{b+m}=1\\ \frac{x}{a+n}+\frac{y}{b+n}=1\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}x=\frac{(a+m)(a+n)}{a+b}\\ y=\frac{(b+m)(b+n)}{a+b}\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=\frac{(a+m)(b+m)}{a-b}\\ y=\frac{(a+n)(b+n)}{a-b}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}x=\frac{(a+m)(a+n)}{a-b}\\ y=\frac{(b+m)(b+n)}{a-b}\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=\frac{(a+m)(a+n)}{a-b}\\ y=-\frac{(b+m)(b+n)}{a-b}\end{array}\right.$ |
20.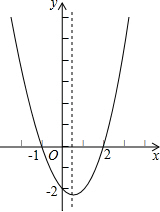 二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
 二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )| A. | 函数有最小值 | B. | 对称轴是直线x=$\frac{1}{2}$ | ||
| C. | 当x<$\frac{1}{2}$时,y随x的增大而减小 | D. | 当-1<x<3时,y>0 |