题目内容
10.先观察、验证,再解答后面的问题:1=$\frac{1}{2}$(1×2-0×1),2=$\frac{1}{2}$(2×3-1×2),3=$\frac{1}{2}$(3×4-2×3),…,n=$\frac{1}{2}$[n(n+1)-(n-1)n].
把上面的n个等式左右两边分别相加,得1+2+3+…+n=$\frac{1}{2}$n(n+1),其中n为正整数.
这样的方法叫叠加法.类比这种方法,
有:1×2=$\frac{1}{3}$(1×2×3-0×1×2),
2×3=$\frac{1}{3}$(2×3×4-1×2×3),
3×4=$\frac{1}{3}$(3×4×5-2×3×4),
将这三个等式左右两边分别相加,得:1×2+2×3+3×4=$\frac{1}{3}$×3×4×5=20.
解答下列问题:
(1)填空:
①1×2+2×3+…+10×11=440;
②1×2+2×3+…+n(n+1)=$\frac{1}{3}n(n+1)(n+2)$;
(2)计算:1×3+3×5+5×7+…+(2n-1)(2n+1),其中n为正整数,结果用n的多项式表示;
(3)证明:12+22+32+…+n2=$\frac{1}{6}$n(n+1)(2n+1),其中n为正整数.
分析 分别根据规律相加计算即可.
解答 解:(1)①1×2+2×3+…+10×11=$\frac{1}{3}$×10×11×12=110×4=440;
②∵1×2+2×3=$\frac{1}{3}$×2×3×4=8,
1×2+2×3+3×4=$\frac{1}{3}$×3×4×5=20,
1×2+2×3+3×4+4×5=$\frac{1}{3}$×4×5×6=40,
…
∴1×2+2×3+…+n(n+1)=$\frac{1}{3}$n(n+1)(n+2),
故答案为:①440;②$\frac{1}{3}$n(n+1)(n+2);
(2)∵1×3=(2×1-1)(2×1+1)=4×12-1,
3×5=(2×2-1)(2×2+1)=4×22-1,
5×7=(2×3-1)(2×3+1)=4×32-1,
…
1×3+3×5+5×7+…+(2n-1)(2n+1),
=4×12-1+4×22-1+4×32-1+…+4×n2-1,
=4×(12+22+32+…+n2)-n,
=4×$\frac{1}{6}$n(n+1)(2n+1)-n,
=$\frac{2}{3}$n(n+1)(2n+1)-n;
(3)∵(n+1)3-n3=3n2+3n+1,
∴当n=1时,23-13=3×12+3×1+1,
当n=2时,33-23=3×22+3×2+1,
当n=3时,43-33=3×32+3×3+1,
…
当n=n时,(n+1)3-n3=3n2+3n+1,
把以下的n个等式相加得:(n+1)3-1=3(12+22+32+…+n2)+3(1+2+3+…+n)+n,
所以,3(12+22+32+…+n2)=(n+1)3-(n+1)-3×$\frac{n(n+1)}{2}$,
即:12+22+32+…+n2=$\frac{1}{6}$n(n+1)(2n+1).
点评 本题是数字类的规律题,此类题要认真观察已知所给的式子,依次的规律和计算的方法,先观察、验证,再解答.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案| A. | 3a+5b=15ab | B. | (a2)3=a9 | C. | a6-a2=a4 | D. | 2a×3a=6a2 |
| A. | $\sqrt{4}$=±2 | B. | ($\frac{1}{2}$)-2=-4 | C. | $\root{3}{-\frac{8}{125}}$=-$\frac{2}{5}$ | D. | (3-$\sqrt{9}$)0=1 |
| A. | 5 | B. | $\sqrt{7}$ | C. | 5或$\sqrt{7}$ | D. | 5或$\sqrt{8}$ |
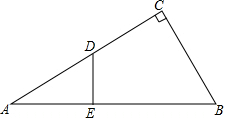 在△ABC中,∠ACB=90°,DE⊥AB,
在△ABC中,∠ACB=90°,DE⊥AB,