题目内容
19.已知tan2α-(1+$\sqrt{3}$)tanα+$\sqrt{3}$=0,求锐角α的度数.分析 首先求得tanα的值,然后根据特殊角的三角函数值即可求解.
解答 解:原式即(tanα-1)(tanα-$\sqrt{3}$)=0,
则tanα=1或tanα=$\sqrt{3}$.
则α=45°或60°.
点评 本题考查了特殊角的三角函数值,正确求得tanα的值是关键.

练习册系列答案
相关题目
9.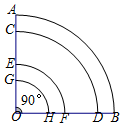 如图,弧$\widehat{AB}$、$\widehat{CD}$、$\widehat{EF}$、$\widehat{GH}$均为以O点为圆心所画出的四个相异弧,其度数均为90°,且G在OA上,C、E在AG上,若AC=EG,OG=2,AG=4,则弧$\widehat{EF}$与弧$\widehat{CD}$的长的和为( )
如图,弧$\widehat{AB}$、$\widehat{CD}$、$\widehat{EF}$、$\widehat{GH}$均为以O点为圆心所画出的四个相异弧,其度数均为90°,且G在OA上,C、E在AG上,若AC=EG,OG=2,AG=4,则弧$\widehat{EF}$与弧$\widehat{CD}$的长的和为( )
 如图,弧$\widehat{AB}$、$\widehat{CD}$、$\widehat{EF}$、$\widehat{GH}$均为以O点为圆心所画出的四个相异弧,其度数均为90°,且G在OA上,C、E在AG上,若AC=EG,OG=2,AG=4,则弧$\widehat{EF}$与弧$\widehat{CD}$的长的和为( )
如图,弧$\widehat{AB}$、$\widehat{CD}$、$\widehat{EF}$、$\widehat{GH}$均为以O点为圆心所画出的四个相异弧,其度数均为90°,且G在OA上,C、E在AG上,若AC=EG,OG=2,AG=4,则弧$\widehat{EF}$与弧$\widehat{CD}$的长的和为( )| A. | 2π | B. | $\frac{8π}{3}$ | C. | $\frac{7π}{2}$ | D. | 4π |
11.方程$\frac{33}{32}$x-2=$\frac{1}{32}$x的解是( )
| A. | x=2 | B. | x=$\frac{1}{2}$ | C. | x=1 | D. | x=32 |
10.在△ABC中,AB=5,BC=8,则AC边的长不可能是( )
| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
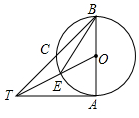 如图,已知AB是⊙O的直径,AT与⊙O相切于点A.⊙O交BT于C,AB=AT,OT交⊙O于E,连BE.求tan∠TBE的值.
如图,已知AB是⊙O的直径,AT与⊙O相切于点A.⊙O交BT于C,AB=AT,OT交⊙O于E,连BE.求tan∠TBE的值.