题目内容
2.在△ABC中,AB=3,BC=4,若△ABC是直角形,则AC的长应是( )| A. | 5 | B. | $\sqrt{7}$ | C. | 5或$\sqrt{7}$ | D. | 5或$\sqrt{8}$ |
分析 由于直角三角形的斜边不确定,故应分BC是直角边与斜边两种情况进行讨论.
解答 解:当BC为直角边时,AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5;
当BC为斜边时,AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$.
综上所述,AC的长为5或$\sqrt{7}$.
故选C.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
11.方程$\frac{33}{32}$x-2=$\frac{1}{32}$x的解是( )
| A. | x=2 | B. | x=$\frac{1}{2}$ | C. | x=1 | D. | x=32 |
10.在△ABC中,AB=5,BC=8,则AC边的长不可能是( )
| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
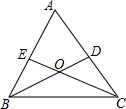 如图,△ABC中,BD、CE是△ABC的角平分线,若∠A=70°,求∠BOC的度数.
如图,△ABC中,BD、CE是△ABC的角平分线,若∠A=70°,求∠BOC的度数.