题目内容

18．分解因式：
（1）-x4+16y4；
（2）（3a-b）2-4（a-b）2．
（3）16（x+y）2-49（x-y）2．

分析 （1）原式利用平方差公式分解即可；
（2）原式利用平方差公式分解即可；
（3）原式利用平方差公式分解即可．

解答 解：（1）原式=（4y2+x2）（2y+x）（2y-x）；
（2）原式=[（3a-b）+2（a-b）][（3a-b）-2（a-b）]=（5a-3b）（a+b）；
（3）原式=[4（x+y）+7（x-y）][4（x+y）-7（x-y）]=（11x-3y）（-3x+11y）．

点评 此题考查了因式分解-运用公式法，熟练掌握因式分解的方法是解本题的关键．

练习册系列答案
相关题目
8．数学课堂上，王老师给同学们出了道题：若（x2-px+3）（x-q）中不含x2项，请同学们探究一下p与q的关系．请你根据所学知识帮助同学们解决一下．
9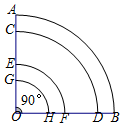．如图，弧$\widehat{AB}$、$\widehat{CD}$、$\widehat{EF}$、$\widehat{GH}$均为以O点为圆心所画出的四个相异弧，其度数均为90°，且G在OA上，C、E在AG上，若AC=EG，OG=2，AG=4，则弧$\widehat{EF}$与弧$\widehat{CD}$的长的和为（　　）
A．2πB．$\frac{8π}{3}$C．$\frac{7π}{2}$D．4π
6．已知a，b互为相反数，c，d互为倒数，x的绝对值为5，求cd+$\frac{a+b}{2016}$-2x的值．
13．海口市某校七年级有5名教师带学生去公园秋游，公园的门票为每人30元，现有两种优惠方案，甲方案：带队教师免费，学生按8折收费；乙方案：师生都按7.5折收费．
（1）若有m名学生，则用式子表示两种优惠方案各需要多少元？
（2）当m=40时，采用哪种方案优惠？
（3）当m=100时，采用哪种方案优惠？
3．下列由四舍五入法得到的近似数各精确到哪一位？
（1）396；
（2）0.054；
（3）5.80亿；
（4）4.30×102．
10．先观察、验证，再解答后面的问题：
1=$\frac{1}{2}$（1×2-0×1），2=$\frac{1}{2}$（2×3-1×2），3=$\frac{1}{2}$（3×4-2×3），…，n=$\frac{1}{2}$[n（n+1）-（n-1）n]．
把上面的n个等式左右两边分别相加，得1+2+3+…+n=$\frac{1}{2}$n（n+1），其中n为正整数．
这样的方法叫叠加法．类比这种方法，
有：1×2=$\frac{1}{3}$（1×2×3-0×1×2），
2×3=$\frac{1}{3}$（2×3×4-1×2×3），
3×4=$\frac{1}{3}$（3×4×5-2×3×4），
将这三个等式左右两边分别相加，得：1×2+2×3+3×4=$\frac{1}{3}$×3×4×5=20．
解答下列问题：
（1）填空：
①1×2+2×3+…+10×11=440；
②1×2+2×3+…+n（n+1）=$\frac{1}{3}n（n+1）（n+2）$；
（2）计算：1×3+3×5+5×7+…+（2n-1）（2n+1），其中n为正整数，结果用n的多项式表示；
（3）证明：12+22+32+…+n2=$\frac{1}{6}$n（n+1）（2n+1），其中n为正整数．
7．一个一次函数的图象，与直线y=2x+1的交点M的横坐标为2，与直线y=-x+2的交点N的横坐标为1，求这个一次函数的解析式．
10．在△ABC中，AB=5，BC=8，则AC边的长不可能是（　　）
A．8B．10C．12D．14

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网