题目内容

1．小明计算一个多边形的内角和时误把一个外角加进去了，得其和为2260°．
①求这个多加的外角的度数．
②求这个多边形对角线的总条数．

分析 ①根据多边形的内角和公式（n-2）•180°可知，多边形的内角和是180°的倍数，然后求出多边形的边数以及多加的外角的度数即可得解；
②根据n边形的对角线的条数是$\frac{n（n-3）}{2}$．

解答 解：①解：设多边形的边数为n，多加的外角度数为α，则
（n-2）•180°=2260°-α，
∵2260°=12×180°+100°，内角和应是180°的倍数，
∴同学多加的一个外角为100°，
∴这是12+2=14边形的内角和．
  ②多边形的对角线的条数是$\frac{14×（14-3）}{2}$=77（条）．
即共有77条对角线．

点评 本题考查了多边形的内角和公式，根据多边形的内角和公式判断出多边形的内角和公式是180°的倍数是解题的关键．

练习册系列答案
相关题目
11．如图，在菱形纸片ABCD中，∠A=60°，折叠菱形纸片ABCD，使点C落在DP（P为AB的中点）所在的直线上，得到经过点D的折痕DE，则∠CDE的度数为45°．
12．画数轴，把下列各数在数轴上表示出来，并用“＜”连接各数．
-|-3.5|，1$\frac{1}{2}$，0，-（-2$\frac{1}{2}$），-（+1）．
9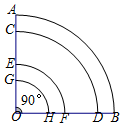．如图，弧$\widehat{AB}$、$\widehat{CD}$、$\widehat{EF}$、$\widehat{GH}$均为以O点为圆心所画出的四个相异弧，其度数均为90°，且G在OA上，C、E在AG上，若AC=EG，OG=2，AG=4，则弧$\widehat{EF}$与弧$\widehat{CD}$的长的和为（　　）
A．2πB．$\frac{8π}{3}$C．$\frac{7π}{2}$D．4π
16．计算：
（1）5+（-5）；
（2）-23+（+58）-（-5）；
（3）-4+28-（-29）+（-24）；          
（4）（-49）-（+91）-（-5）+（-9）；
（5）-7.2-0.8-5.6+11.6；            
（6）（-$\frac{6}{5}$）-（-0.2）+1；
（7）|-3+1|-（-2）；
（8）$\frac{1}{6}$+（-$\frac{2}{7}$）+（+$\frac{5}{6}$）+（-$\frac{5}{7}$）．
6．已知a，b互为相反数，c，d互为倒数，x的绝对值为5，求cd+$\frac{a+b}{2016}$-2x的值．
13．海口市某校七年级有5名教师带学生去公园秋游，公园的门票为每人30元，现有两种优惠方案，甲方案：带队教师免费，学生按8折收费；乙方案：师生都按7.5折收费．
（1）若有m名学生，则用式子表示两种优惠方案各需要多少元？
（2）当m=40时，采用哪种方案优惠？
（3）当m=100时，采用哪种方案优惠？
10．先观察、验证，再解答后面的问题：
1=$\frac{1}{2}$（1×2-0×1），2=$\frac{1}{2}$（2×3-1×2），3=$\frac{1}{2}$（3×4-2×3），…，n=$\frac{1}{2}$[n（n+1）-（n-1）n]．
把上面的n个等式左右两边分别相加，得1+2+3+…+n=$\frac{1}{2}$n（n+1），其中n为正整数．
这样的方法叫叠加法．类比这种方法，
有：1×2=$\frac{1}{3}$（1×2×3-0×1×2），
2×3=$\frac{1}{3}$（2×3×4-1×2×3），
3×4=$\frac{1}{3}$（3×4×5-2×3×4），
将这三个等式左右两边分别相加，得：1×2+2×3+3×4=$\frac{1}{3}$×3×4×5=20．
解答下列问题：
（1）填空：
①1×2+2×3+…+10×11=440；
②1×2+2×3+…+n（n+1）=$\frac{1}{3}n（n+1）（n+2）$；
（2）计算：1×3+3×5+5×7+…+（2n-1）（2n+1），其中n为正整数，结果用n的多项式表示；
（3）证明：12+22+32+…+n2=$\frac{1}{6}$n（n+1）（2n+1），其中n为正整数．
11．方程$\frac{33}{32}$x-2=$\frac{1}{32}$x的解是（　　）
A．x=2B．x=$\frac{1}{2}$C．x=1D．x=32

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网