题目内容
9.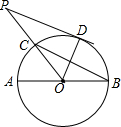 如图,AB是⊙O的直径,BC是弦,∠ABC=30°,连结OC并延长至点P,使CP=OC,过点P作⊙O的切线,D是切点.
如图,AB是⊙O的直径,BC是弦,∠ABC=30°,连结OC并延长至点P,使CP=OC,过点P作⊙O的切线,D是切点.(Ⅰ)求证:PD∥BC;
(Ⅱ)当BC=3时,求PD的长.
分析 (1)连接CD.由切线的性质可知PD⊥OD,然后依据直角三角形斜边上中线的性质和圆的性质证明△CDO为等边三角形,接下来,在求得∠CEO=90°,最后依据平行线的判定定理证明即可
(2)记BC与OD的交点为E.先求得CE的长,然后由CB∥PD可知△OCE∽△OPD,接下来,依据相似三角形的性质可求得PD的长.
解答 解:(1)如图1所示:连接CD.
∵PD是圆O的切线,D为切线,
∴OD⊥PD.
∵在Rt△PDO中,C为PO的中点,
∴CD=OC.
∵CO=OD,
∴CD=OC=DO,
∴∠COD=60°.
∵OC=OB,
∴∠OCB=∠OBC=30°.
∴∠OEC=180°-30°-60°=90°.
∴∠OEC=∠ODP=90°.
∴BC∥PD.
(2)如图2所示:记BC与OD的交点为E.
∵OC=OB,OD⊥BC,
∴CE=$\frac{1}{2}$BC=$\frac{3}{2}$.
∵C是OP的中点,
∴$\frac{OC}{OP}$=$\frac{1}{2}$.
∵BC∥PD,
∴△OCE∽△OPD.
∴$\frac{CE}{PD}=\frac{OC}{OP}$,即$\frac{\frac{3}{2}}{PD}=\frac{1}{2}$.
解得:PD=3.
所以PD的长为3.
点评 本题主要考查的是切线的性质、等腰三角形的性质、等边三角形的性质、相似三角形的性质和判定、直角三角形斜边上中线的性质,证得△CDO为等边三角形是解题的关键.

练习册系列答案
相关题目
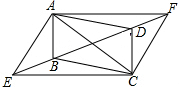 如图,已知四边形AECF是平行四边形,点B,D在对角线EF上,且BE=DF,用向量的加法证明:四边形ABCD是平行四边形.
如图,已知四边形AECF是平行四边形,点B,D在对角线EF上,且BE=DF,用向量的加法证明:四边形ABCD是平行四边形.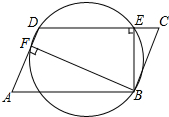 如图,在?ABCD中,BE⊥CD,BF⊥AD,垂足分别是点E,F.求证:B,E,D,F四点都在同一个圆上.
如图,在?ABCD中,BE⊥CD,BF⊥AD,垂足分别是点E,F.求证:B,E,D,F四点都在同一个圆上.