题目内容
11.如图,已知四边形ABCD菱形,点E、F、G、H分别在菱形的四条边上,且AE=CG,AH=CF.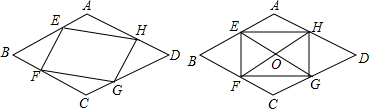
(1)求证:四边形EFGH是平行四边形;
(2)若点E、F、G、H分别是菱形ABCD四条边的中点,连接EG、FH相交于点O,请写出图中除菱形ABCD外的所有菱形.
分析 (1)根据菱形的性质得出∠A=∠C,∠B=∠D,AD=CD=BC=AB,求出BE=DG,BF=DH,根据SAS推出△AEH≌△CGF,根据全等得出EH=FG,同理EF=HG,根据平行四边形的判定得出即可;
(2)根据菱形的性质得出AB=BC=CD=AD,AC⊥BD,根据直角三角形的斜边上中线性质得出OE=$\frac{1}{2}$AB=AE=BE,OH=$\frac{1}{2}$AD=AH=DH,OG=$\frac{1}{2}$DC=DG=CG,OF=$\frac{1}{2}$BC=CF=BF,求出OE=BE=BF=OF,OF=FC=CG=OG,OG=GD=DH=OH,OE=AE=AH=OH,根据菱形的判定得出即可.
解答 (1)证明:∵四边形ABCD是菱形,
∴∠A=∠C,∠B=∠D,AD=CD=BC=AB,
∵AE=CG,AH=CF,
∴BE=DG,BF=DH,
在△AEH和△CGF中
$\left\{\begin{array}{l}{AE=CG}\\{∠A=∠C}\\{AH=CF}\end{array}\right.$
∴△AEH≌△CGF(SAS),
∴EH=FG,
同理EF=HG,
∴四边形EFGH是平行四边形;
(2)解:如图2,连接AC和BD,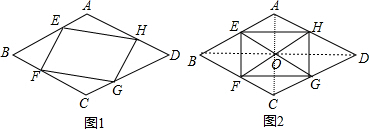
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥BD,
∵点E、F、G、H分别是菱形ABCD四条边的中点,
∴OE=$\frac{1}{2}$AB=AE=BE,OH=$\frac{1}{2}$AD=AH=DH,OG=$\frac{1}{2}$CD=DG=CG,OF=$\frac{1}{2}$BC=CF=BF,
∴OE=BE=BF=OF,OF=FC=CG=OG,OG=GD=DH=OH,OE=AE=AH=OH,
∴四边形OEBF、OFCG、OGDH、OHAE都是菱形,
即除菱形ABCD外的所有菱形有四边形OEBF、四边形OFCG、四边形OGDH、四边形OHAE.
点评 本题考查了三角形的中位线,菱形的性质和判定,平行四边形的性质的应用,能综合运用定理进行推理是解此题的关键.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案| A. | 3和-2 | B. | -3和2 | C. | 3和2 | D. | -3和-2 |
| A. | 1:4 | B. | 1:2 | C. | 1:16 | D. | 无法确定 |
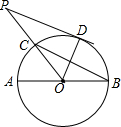 如图,AB是⊙O的直径,BC是弦,∠ABC=30°,连结OC并延长至点P,使CP=OC,过点P作⊙O的切线,D是切点.
如图,AB是⊙O的直径,BC是弦,∠ABC=30°,连结OC并延长至点P,使CP=OC,过点P作⊙O的切线,D是切点. 如图,在平行四边形ABCD中,AB⊥AC,点E是AC上一点,且AE=AB,连接BE交BC边上的高AF于点H,延长对角线CA至点G.使AG=CE,连接GH.求证:∠CAD=∠G.
如图,在平行四边形ABCD中,AB⊥AC,点E是AC上一点,且AE=AB,连接BE交BC边上的高AF于点H,延长对角线CA至点G.使AG=CE,连接GH.求证:∠CAD=∠G.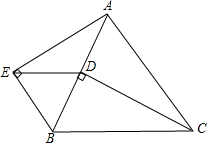 如图,△ABC是等边三角形,CD⊥AB于点D,∠AEB=90°,CD=AE,求证:△EBD是等边三角形.
如图,△ABC是等边三角形,CD⊥AB于点D,∠AEB=90°,CD=AE,求证:△EBD是等边三角形.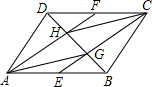 如图,ABCD为平行四边形,E、F分别为AB、CD的中点.
如图,ABCD为平行四边形,E、F分别为AB、CD的中点.