��Ŀ����
17����ͼ1��PΪ��MONƽ����OC��һ�㣬��PΪ����ġ�APB���߷ֱ�������OM��ON����A��B���㣬�����APB���Ƶ�P��תʱʼ������OA•OB=OP2�����ǾͰѡ�APB������MON�Ĺ����ǣ���1����ͼ2��PΪ��MONƽ����OC��һ�㣬��P��PB��ON��B��AP��OC��P����ô��APB�ǡ�MON�Ĺ����ǣ���ǡ����ǡ�����
��2������ͼ3�������MON=60�㣬OP=2����APB�ǡ�MON�Ĺ����ǣ�����AB�����AOB������͡�APB�Ķ�����
�������MON=���㣨0�㣼���㣼90�㣩��OP=m����APB�ǡ�MON�Ĺ����ǣ�ֱ���ú��Ц���m�Ĵ���ʽ��ʾ��AOB�������
��3����ͼ4����C�Ǻ���y=$\frac{2}{x}$��x��0��ͼ����һ�����㣬����C��ֱ��CD�ֱ�x���y����A��B���㣬������BC=2CA��ֱ��д����AOB�Ĺ����ǡ�APB�Ķ���P�����꣮
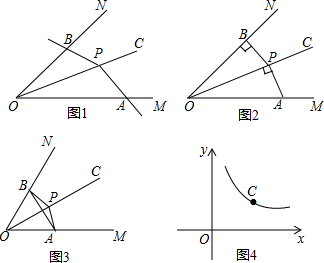
���� ��1�����жϳ���OBP�ס�OPA�����ɣ�
��2���ȸ��ݹ��������OA��OB=4�������������ε������ʽ���Լ����ƣ��õ���OAP=��OPB�����ɣ�
��3������������������ۣ���B��y������������ᣬ�ڸ�����ʱ���������㣬�����ڣ�����������ʱ����BC=2AC�жϳ���C���߶�AB��һ�����ȷֵ㣬���ɣ�
��� �⣺��1����PΪ��MONƽ����OC��һ�㣬
���BOP=��AOP��
��PB��ON��B��AP��OC��P��
���OBP=��OPA��
���OBP�ס�OPA��
��$\frac{OB}{OP}=\frac{OP}{OA}$��
��OP2=OA��OB��
���APB�ǡ�MON�Ĺ����ǣ�
�ʴ�Ϊ�ǣ�
��2������ͼ������A��AH��OB��
�ߡ�APB�ǡ�MON�Ĺ����ǣ�OP=2��
��OA��OB=OP2=4��
��Rt��AOH�У���AOH=90�㣬
��sin��AOH=$\frac{AH}{OA}$��
��AH=OAsin��AOH��
��S��AOB=$\frac{1}{2}$OB��AH=$\frac{1}{2}$OB��OA��sin60��=$\frac{1}{2}$��OP2��$\frac{\sqrt{3}}{2}$=$\sqrt{3}$��
��OP2=OA��OB��
��$\frac{OA}{OP}=\frac{OP}{OB}$��
�ߵ�PΪ��MON��ƽ������һ�㣬
���AOP=��BOP=$\frac{1}{2}$��MON=30�㣬
���AOP�ס�POB��
���OAP=��OPB��
���APB=��OPB+��OPA=��OAP+��OPA=180��-30��=150�㣬
���ɢ��У�S��AOB=$\frac{1}{2}$OB��OA����MON=$\frac{1}{2}$m2��sin����
��3���߹���C��ֱ��CD�ֱ�x���y����A��B���㣬������BC=2CA��
��ֻ�е�A��x�������ᣬ
�ٵ���B��y�Ḻ����ʱ����Aֻ����x�������ᣮ������Pֻ���ڵ������ޣ�
��A��m��0����B��0��n����m��0��n��0��
��OA=m��OB=-n��
��BC=2CA��
���A��BC�е㣬
���C��2m��-n����
�ߵ�C��˫����y=$\frac{2}{x}$�ϣ�
��2m����-n��=2��
��mn=-1��
�ߡ�AOB�Ĺ����ǡ�APB
��OP2=OA��OB=|m|•|n|=1��
��OP=1��
�ߵ�P�ڡ�AOB��ƽ�����ϣ���P��a��-a����a��0����
��OP2=2a2��
��2a2=1��
��a=$\frac{\sqrt{2}}{2}$��a=-$\frac{\sqrt{2}}{2}$���ᣩ��
���P��$\frac{\sqrt{2}}{2}$��-$\frac{\sqrt{2}}{2}$��
�ڵ���B��y�������ᣬ����BC=2CA�����ԣ���Aֻ����x���������ϣ�
��A��m��0����B��0��n����m��0��n��0��
���C��$\frac{2m}{3}$��$\frac{n}{3}$����
��$\frac{2m}{3}��\frac{n}{3}$=2��
��mn=9��
�ߡ�AOB�Ĺ����ǡ�APB
��OP2=OA��0B=mn=9��
��OP=3��
�ߵ�P�ڡ�AOB��ƽ�����ϣ�������P�ڵ�һ���ޣ���P��a��a������a��0��
��OP2=2a2��
��2a2=9��
��a=$\frac{3\sqrt{2}}{2}$��a=-$\frac{3\sqrt{2}}{2}$���ᣩ
������P��$\frac{3\sqrt{2}}{2}$��$\frac{3\sqrt{2}}{2}$����
������������$\frac{\sqrt{2}}{2}$��-$\frac{\sqrt{2}}{2}$����$\frac{3\sqrt{2}}{2}$��$\frac{3\sqrt{2}}{2}$����
���� �����Ǽ��α任�ۺ��⣬��Ҫ�������¶��壬�����ǵ�����ͼ�Ӧ�ã����������ε��ж������ʣ������ǵ������ǽⱾ��Ĺؼ���

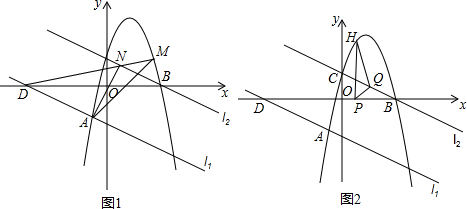
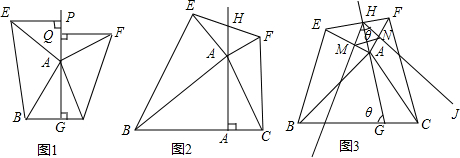
 ��ͼ��������ABCD�У���ABC=��BAD=90�㣬��AD��ȡһ��E������ABE��ֱ��BE�۵���ʹ��A����BD�ϵ�G����EG���ӳ��߽�ֱ��BC�ڵ�F��
��ͼ��������ABCD�У���ABC=��BAD=90�㣬��AD��ȡһ��E������ABE��ֱ��BE�۵���ʹ��A����BD�ϵ�G����EG���ӳ��߽�ֱ��BC�ڵ�F�� ��ֱ֪������ABCD�У�AD��BC��AB��BC��AD=4��BC=DC=5����P��BC���ƶ�����PA+PDȡ��Сֵʱ��BP��Ϊ��������
��ֱ֪������ABCD�У�AD��BC��AB��BC��AD=4��BC=DC=5����P��BC���ƶ�����PA+PDȡ��Сֵʱ��BP��Ϊ��������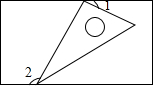 ��ͼ����һ������30��ǵ�ֱ�������ε������������һ�����εĶԱ��ϣ�����1=35�㣬���2=125�㣮
��ͼ����һ������30��ǵ�ֱ�������ε������������һ�����εĶԱ��ϣ�����1=35�㣬���2=125�㣮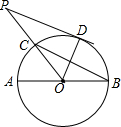 ��ͼ��AB�ǡ�O��ֱ����BC���ң���ABC=30�㣬����OC���ӳ�����P��ʹCP=OC������P����O�����ߣ�D���е㣮
��ͼ��AB�ǡ�O��ֱ����BC���ң���ABC=30�㣬����OC���ӳ�����P��ʹCP=OC������P����O�����ߣ�D���е㣮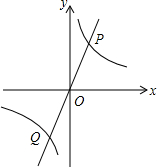 ��ͼ������������y=mx�뷴��������y=$\frac{k}{x}$��ͼ���ཻ��P��Q���㣬PA��x����A����PAO�������3��
��ͼ������������y=mx�뷴��������y=$\frac{k}{x}$��ͼ���ཻ��P��Q���㣬PA��x����A����PAO�������3��