题目内容

4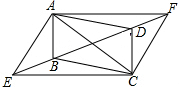．如图，已知四边形AECF是平行四边形，点B，D在对角线EF上，且BE=DF，用向量的加法证明：四边形ABCD是平行四边形．

分析 根据向量的三角形法则表示出$\overrightarrow{EB}$，$\overrightarrow{DF}$，然后整理可得$\overrightarrow{AB}$+$\overrightarrow{AD}$=$\overrightarrow{AE}$+$\overrightarrow{AF}$，再根据平行四边形法则证明．

解答 证明：由三角形法则得，$\overrightarrow{EB}$=$\overrightarrow{AB}$-$\overrightarrow{AE}$，
$\overrightarrow{DF}$=$\overrightarrow{AF}$-$\overrightarrow{AD}$，
∵点B，D在对角线EF上，且BE=DF，
∴$\overrightarrow{EB}$=$\overrightarrow{DF}$，
∴$\overrightarrow{AB}$-$\overrightarrow{AE}$=$\overrightarrow{AF}$-$\overrightarrow{AD}$，
∴$\overrightarrow{AB}$+$\overrightarrow{AD}$=$\overrightarrow{AE}$+$\overrightarrow{AF}$，
∵四边形AECF是平行四边形，
∴$\overrightarrow{AE}$+$\overrightarrow{AF}$=$\overrightarrow{AC}$，
∴$\overrightarrow{AB}$+$\overrightarrow{AD}$=$\overrightarrow{AC}$，
∴四边形ABCD是平行四边形．

点评 本题考查了平面向量，平行四边形的判定与性质，向量的问题，熟练掌握平行四边形法则和三角形法则是解题的关键．

练习册系列答案
相关题目
14．计算：若ab＞0，求$\frac{a}{|a|}$+$\frac{b}{|b|}$+$\frac{|ab|}{ab}$的值．
15．解方程$1-\frac{x+3}{3}=\frac{x}{2}$时，去分母后可以得到（　　）
A．1-x-3=3xB．6-2x-6=3xC．6-x+3=3xD．1-x+3=3x
12．已知直角梯形ABCD中，AD∥BC，AB⊥BC，AD=4，BC=DC=5，点P在BC上移动，则当PA+PD取最小值时，BP长为（　　）
A．1B．2C．2.5D．3
19．如图1，四边形ABCD中，AB=AD，BC=CD，我们把这种两组邻边分别相等的四边形叫做筝形．请探究“筝形”的性质和判定方法．小聪根据学习四边形的经验，对“筝形”的判定和性质进行了探究．
下面是小聪的探究过程，请补充完整：
（1）如图2，连接筝形ABCD的对角线AC，BD交于点O，通过测量边、角或沿一条对角线所在直线折叠等方法探究发现筝形有一组对角相等，请写出筝形的其他性质（一条即可）：对角线互相垂直，这条性质可用符号表示为：已知四边形ABCD是筝形，则AC⊥BD．；
（2）从边、角、对角线或性质的逆命题等角度进行探究，写出筝形的一个判定方法（定义除外），并证明你的结论．
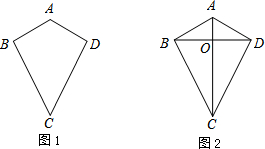
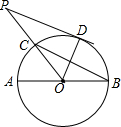9．如图，AB是⊙O的直径，BC是弦，∠ABC=30°，连结OC并延长至点P，使CP=OC，过点P作⊙O的切线，D是切点．
（Ⅰ）求证：PD∥BC；
（Ⅱ）当BC=3时，求PD的长．
16．如图，AB为⊙0的直径，$\widehat{BC}$=$\widehat{CD}$，CE⊥AD于E，OE交AC于点F．
（1）求证：CE与⊙O相切；
（2）若cos∠BAD=$\frac{4}{5}$，求$\frac{AF}{FC}$的值．
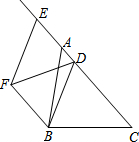5．如图，△ABC中，AB=10，sin∠BAC=$\frac{3}{5}$，点D为边AC上一点，点E为CA延长线上一点，且$\frac{AD}{AE}$=$\frac{1}{2}$，以DB、DE为边作?BDEF，则当对角线DF的长取得最小值时，BD的长为8．
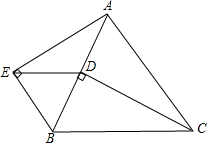6．如图，△ABC是等边三角形，CD⊥AB于点D，∠AEB=90°，CD=AE，求证：△EBD是等边三角形．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网