题目内容
1.已知关于x、y的方程组$\left\{\begin{array}{l}{x-y=3k+1}\\{x+y=3+k}\end{array}\right.$的解满足$\left\{\begin{array}{l}{x>0}\\{y<0}\end{array}\right.$,求k的取值范围.分析 先解方程组求得方程组的解,然后由给出的x>0,y>0,列出不等式方程组,再解不等式组即可.
解答 解:解方程组可得$\left\{\begin{array}{l}{x=2k+2}\\{y=1-k}\end{array}\right.$,
∵方程组的解满足$\left\{\begin{array}{l}{x>0}\\{y<0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{2k+2>0}\\{1-k<0}\end{array}\right.$,
解得:k>1.
点评 本题主要考查的是二元一次方程组的解、解一元一次不等式,求得方程组的解是解题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
3.如果3x2n-1ym与-5xmyn+1是同类项,则m和n的值分别为( )
| A. | 3和-2 | B. | -3和2 | C. | 3和2 | D. | -3和-2 |
 已知直角梯形ABCD中,AD∥BC,AB⊥BC,AD=4,BC=DC=5,点P在BC上移动,则当PA+PD取最小值时,BP长为( )
已知直角梯形ABCD中,AD∥BC,AB⊥BC,AD=4,BC=DC=5,点P在BC上移动,则当PA+PD取最小值时,BP长为( )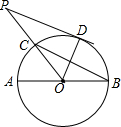 如图,AB是⊙O的直径,BC是弦,∠ABC=30°,连结OC并延长至点P,使CP=OC,过点P作⊙O的切线,D是切点.
如图,AB是⊙O的直径,BC是弦,∠ABC=30°,连结OC并延长至点P,使CP=OC,过点P作⊙O的切线,D是切点. 如图,AB为⊙0的直径,$\widehat{BC}$=$\widehat{CD}$,CE⊥AD于E,OE交AC于点F.
如图,AB为⊙0的直径,$\widehat{BC}$=$\widehat{CD}$,CE⊥AD于E,OE交AC于点F.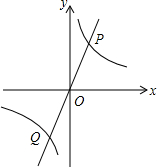 如图,正比例函数y=mx与反比例函数y=$\frac{k}{x}$的图象相交于P、Q两点,PA⊥x轴于A,△PAO的面积是3.
如图,正比例函数y=mx与反比例函数y=$\frac{k}{x}$的图象相交于P、Q两点,PA⊥x轴于A,△PAO的面积是3.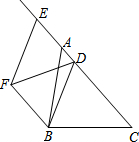 如图,△ABC中,AB=10,sin∠BAC=$\frac{3}{5}$,点D为边AC上一点,点E为CA延长线上一点,且$\frac{AD}{AE}$=$\frac{1}{2}$,以DB、DE为边作?BDEF,则当对角线DF的长取得最小值时,BD的长为8.
如图,△ABC中,AB=10,sin∠BAC=$\frac{3}{5}$,点D为边AC上一点,点E为CA延长线上一点,且$\frac{AD}{AE}$=$\frac{1}{2}$,以DB、DE为边作?BDEF,则当对角线DF的长取得最小值时,BD的长为8. 如图,在平行四边形ABCD中,AB⊥AC,点E是AC上一点,且AE=AB,连接BE交BC边上的高AF于点H,延长对角线CA至点G.使AG=CE,连接GH.求证:∠CAD=∠G.
如图,在平行四边形ABCD中,AB⊥AC,点E是AC上一点,且AE=AB,连接BE交BC边上的高AF于点H,延长对角线CA至点G.使AG=CE,连接GH.求证:∠CAD=∠G.