题目内容
14.关于x的方程:x+$\frac{1}{x}$=c+$\frac{1}{c}$的解为x=c,x=$\frac{-1}{c}$;x+$\frac{1}{x}$=c+$\frac{1}{c}$的解为x=c或x=$\frac{1}{c}$;
x+$\frac{2}{x}$=c+$\frac{2}{c}$的解为x=c,x=$\frac{2}{c}$;
x+$\frac{3}{x}$=c+$\frac{3}{c}$的解为x=c,x=$\frac{3}{c}$;
…
根据材料解决下列问题:
(1)方程x+$\frac{1}{x}$=$\frac{5}{2}$的解是x=2,x=$\frac{1}{2}$;
(2)猜想方程x+$\frac{m}{c}$=c+$\frac{m}{c}$(m≠0)的解,并将所得的解代入方程中检验;
(2)由上述的观察、比较、猜想、验证,可以得出结论:如果方程的左边是未知数与其倒数的倍数的和,方程右边的形式与左边完全相同,只有把其中的未知数换成某个常数,那么这样的方程可以直接得解.
请用这个结论解关于x的方程:x+$\frac{2}{x-1}$=a+$\frac{2}{a-1}$.
分析 (1)由x+$\frac{1}{x}$=$\frac{5}{2}$可得x+$\frac{1}{x}$=2+$\frac{1}{2}$,根据题意可得;
(2)由(1)的形式即可猜想方程的解;代入原方程判断能否是方程两边相等即可;
(3)先将原方程转化为:x-1+$\frac{2}{x-1}$=a-1+$\frac{2}{a-1}$的形式,然后得到:x-1=a-1和x-1=$\frac{2}{a-1}$,然后解得即可.
解答 解:(1)由x+$\frac{1}{x}$=$\frac{5}{2}$可得x+$\frac{1}{x}$=2+$\frac{1}{2}$,
∴该方程的解为:x=2或x=$\frac{1}{2}$;
(2)方程x+$\frac{m}{x}$=c+$\frac{m}{c}$(m≠0)的解为:x=c或x=$\frac{m}{c}$,
检验:当x=c时,左边=c+$\frac{m}{c}$=右边,故x=c是方程的解,
当x=$\frac{m}{c}$时,左边=$\frac{m}{c}$+$\frac{m}{\frac{m}{c}}$=$\frac{m}{c}+c$=右边,故x=$\frac{m}{c}$也是方程的解;
(3)原方程x+$\frac{2}{x-1}$=a+$\frac{2}{a-1}$可化为:
x-1+$\frac{2}{x-1}$=a-1+$\frac{2}{a-1}$
所以x-1=a-1或x-1=$\frac{2}{a-1}$,
解得:x=a或x=$\frac{a+1}{a-1}$,
经检验,x=a或x=$\frac{a+1}{a-1}$是原方程的解,
故答案为:(1)x=2或x=$\frac{1}{2}$.
点评 此题考查了分式方程的解,解题的关键是:将方程转化为:x+$\frac{1}{x}$=c+$\frac{1}{c}$的形式.

| A. | a是实数,且|a|≥0 | B. | $\frac{1}{2}$+$\frac{x-1}{5}$=0不是分式方程 | ||
| C. | 三角形内角和等于360° | D. | a是实数,a0=1 |
 如图,在梯形ABCD中,∠ABC=∠BAD=90°,在AD上取一点E,将△ABE沿直线BE折叠,使点A落在BD上的G处,EG的延长线交直线BC于点F.
如图,在梯形ABCD中,∠ABC=∠BAD=90°,在AD上取一点E,将△ABE沿直线BE折叠,使点A落在BD上的G处,EG的延长线交直线BC于点F.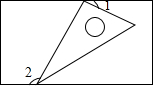 如图,将一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=35°,则∠2=125°.
如图,将一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=35°,则∠2=125°.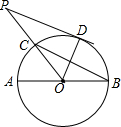 如图,AB是⊙O的直径,BC是弦,∠ABC=30°,连结OC并延长至点P,使CP=OC,过点P作⊙O的切线,D是切点.
如图,AB是⊙O的直径,BC是弦,∠ABC=30°,连结OC并延长至点P,使CP=OC,过点P作⊙O的切线,D是切点.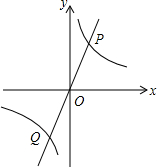 如图,正比例函数y=mx与反比例函数y=$\frac{k}{x}$的图象相交于P、Q两点,PA⊥x轴于A,△PAO的面积是3.
如图,正比例函数y=mx与反比例函数y=$\frac{k}{x}$的图象相交于P、Q两点,PA⊥x轴于A,△PAO的面积是3.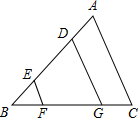 如图,在△ABC中,AD=BE,EF∥DG∥AC.
如图,在△ABC中,AD=BE,EF∥DG∥AC.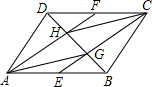 如图,ABCD为平行四边形,E、F分别为AB、CD的中点.
如图,ABCD为平行四边形,E、F分别为AB、CD的中点.