题目内容
10．
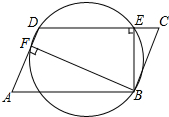如图，在?ABCD中，BE⊥CD，BF⊥AD，垂足分别是点E，F．求证：B，E，D，F四点都在同一个圆上．
分析 欲证明B，E，D，F四点都在同一个圆上，只要找到一个点O，证明OD=OF=OB=0E即可，这个点就是BC中点O．
解答 证明：如图，连接BD取BD的中点O，连接OE、OF．
∵BE⊥CD，BF⊥AD，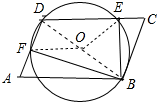
∴∠DEB=∠BFD=90°，
∵DO=OB，
∴OE=OD=OB，OF=OD=0B，
∴OD=OF=OB=OE，
∴B，E，D，F四点都在同一个圆上．
点评 本题考查圆、平行四边形、直角三角形斜边中线性质等知识，解题的关键是选取BD中点O，利用直角三角形斜边中线性质解决问题，属于中考常考题型．
练习册系列答案
优学名师名题系列答案
相关题目
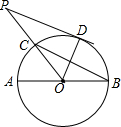如图，AB是⊙O的直径，BC是弦，∠ABC=30°，连结OC并延长至点P，使CP=OC，过点P作⊙O的切线，D是切点．
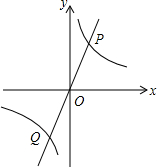如图，正比例函数y=mx与反比例函数y=$\frac{k}{x}$的图象相交于P、Q两点，PA⊥x轴于A，△PAO的面积是3．
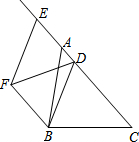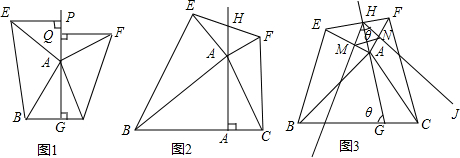
如图，△ABC中，AB=10，sin∠BAC=$\frac{3}{5}$，点D为边AC上一点，点E为CA延长线上一点，且$\frac{AD}{AE}$=$\frac{1}{2}$，以DB、DE为边作?BDEF，则当对角线DF的长取得最小值时，BD的长为8．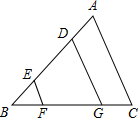
如图，在△ABC中，AD=BE，EF∥DG∥AC．
如图，在平行四边形ABCD中，AB⊥AC，点E是AC上一点，且AE=AB，连接BE交BC边上的高AF于点H，延长对角线CA至点G．使AG=CE，连接GH．求证：∠CAD=∠G．