题目内容
已知x=2是不等式(x-5)(ax-3a+2)≤0的解,且x=1不是这个不等式的解,则实数a的取值范围是( )
A. a>1 B. a≤2 C. 1<a≤2 D. 1≤a≤2
 C
【解析】根据x=2是不等式(x-5)(ax-3a+2)≤0的解,可知(2-5)(2a-3a+2)≤0,解得:a≤2,再根据x=1不是这个不等式的解,可得(1-5)(a-3a+2)>0,解得:a>1,
由此可得a的取值范围为:1<a≤2.
故选:C.
C
【解析】根据x=2是不等式(x-5)(ax-3a+2)≤0的解,可知(2-5)(2a-3a+2)≤0,解得:a≤2,再根据x=1不是这个不等式的解,可得(1-5)(a-3a+2)>0,解得:a>1,
由此可得a的取值范围为:1<a≤2.
故选:C.
练习册系列答案
相关题目
如图所示,H是△ABC的高AD,BE的交点,且DH=DC,则下列结论:①BD=AD;②BC=AC;③BH=AC;④CE=CD中正确的有( )
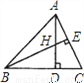
A. 1个 B. 2个 C. 3个 D. 4个
 B
【解析】【解析】
①∵BE⊥AC,AD⊥BC,∴∠AEH=∠ADB=90°.
∵∠HBD+∠BHD=90°,∠EAH+∠AHE=90°,∠BHD=∠AHE,∴∠HBD=∠EAH.
∵DH=DC,∴△BDH≌△ADC(AAS),∴BD=AD,BH=AC;
②∵BC=AC,∴∠BAC=∠ABC.
由①知,在Rt△ABD中,∵BD=AD,∴∠ABC=45°,∴∠BAC...
B
【解析】【解析】
①∵BE⊥AC,AD⊥BC,∴∠AEH=∠ADB=90°.
∵∠HBD+∠BHD=90°,∠EAH+∠AHE=90°,∠BHD=∠AHE,∴∠HBD=∠EAH.
∵DH=DC,∴△BDH≌△ADC(AAS),∴BD=AD,BH=AC;
②∵BC=AC,∴∠BAC=∠ABC.
由①知,在Rt△ABD中,∵BD=AD,∴∠ABC=45°,∴∠BAC... 下列图形经过平移后恰好可以与原图形组合成一个长方形的是( )
A. 三角形 B. 正方形 C. 梯形 D. 都有可能
 B
【解析】试题解析:正方形能够通过平移而得到的新图形和原图形组合成一个长方形.
故选B.
B
【解析】试题解析:正方形能够通过平移而得到的新图形和原图形组合成一个长方形.
故选B. 设a,b,c,d都是整数,且a<2b,b<3c,c<4d,d<20,则a的最大值是( )
A. 480 B. 479 C. 448 D. 447
 D
【解析】由a,b,c,d都是整数,且a<2b,b<3c,c<4d,d<20,可知d=19,c<4×19=76,代入可得c=75,b<3×75=225,再次代入b=224,a<2×224=448,因此可求出a=447,
故选:D.
D
【解析】由a,b,c,d都是整数,且a<2b,b<3c,c<4d,d<20,可知d=19,c<4×19=76,代入可得c=75,b<3×75=225,再次代入b=224,a<2×224=448,因此可求出a=447,
故选:D. 关于x的不等式(a-1)x>a-1的解集为x<1,则下列判断正确的是( )
A. a<0 B. a>1 C. a<1 D. a为任意数
 C
【解析】由含有a的不等式(a-1)x>a-1的解集为:x<1,根据不等式的基本性质3,可知a-1<0,解得a<1.
故选:C.
C
【解析】由含有a的不等式(a-1)x>a-1的解集为:x<1,根据不等式的基本性质3,可知a-1<0,解得a<1.
故选:C. 如图,在△ABC中,∠B与∠C的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E.若AB=5,AC=4,则△ADE的周长是__________.
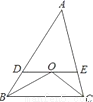
 9
【解析】∵在△ABC中,∠B与∠C的平分线交于点O,
∴∠DBO=∠CBO,∠ECO=∠BCO,
∵DE∥BC,
∴∠DOB=∠CBO,∠EOC=∠BCO,
∴∠DBO=∠DOB,∠ECO=∠EOC,
∴OD=BD,OE=CE,
∵AB=5,AC=4,
∴△ADE的周长为:AD+DE+AE=AD+DO+EO+AE=AD+DB+EC+AE=AB+A...
9
【解析】∵在△ABC中,∠B与∠C的平分线交于点O,
∴∠DBO=∠CBO,∠ECO=∠BCO,
∵DE∥BC,
∴∠DOB=∠CBO,∠EOC=∠BCO,
∴∠DBO=∠DOB,∠ECO=∠EOC,
∴OD=BD,OE=CE,
∵AB=5,AC=4,
∴△ADE的周长为:AD+DE+AE=AD+DO+EO+AE=AD+DB+EC+AE=AB+A... 下面命题不正确的是( )
A. 两个内角分别是50°和65°的三角形是等腰三角形
B. 两个外角相等的三角形是等腰三角形
C. 一个外角的平分线平行于一边的三角形是等腰三角形
D. 两个内角不相等的三角形不是等腰三角形
 D
【解析】解:A.第三个角180°﹣50°﹣65°=65°,有两角相等的三角形是等腰三角形,正确;
B.外角相等,则对应的内角也相等,有两角相等的三角形是等腰三角形,正确;
C.利用两直线平行,内错角相等,同位相等,可知,另外的两内角也相等,有两角相等的三角形是等腰三角形,正确;
D.两个内角不相等的三角形可能是等腰三角形,错误.
故选D.
D
【解析】解:A.第三个角180°﹣50°﹣65°=65°,有两角相等的三角形是等腰三角形,正确;
B.外角相等,则对应的内角也相等,有两角相等的三角形是等腰三角形,正确;
C.利用两直线平行,内错角相等,同位相等,可知,另外的两内角也相等,有两角相等的三角形是等腰三角形,正确;
D.两个内角不相等的三角形可能是等腰三角形,错误.
故选D. 下列哪个多项式能分解成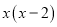 ( )
( )
A. 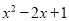 B.
B. 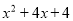 C.
C. 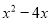 D.
D. 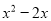
 D
【解析】利用因式分解是整式乘法的逆运算,可知x(x-2)=.
故选:D.
D
【解析】利用因式分解是整式乘法的逆运算,可知x(x-2)=.
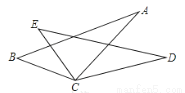
故选:D. 如图,已知BC=EC,∠BCE=∠ACD,要使△ABC≌△DEC,则应添加的一个条件为 (答案不唯一,只需填一个)
 AC=DC或∠B=∠E或∠A=∠D
【解析】试题分析:本题根据∠BCE=∠CAD可得∠BCA=∠ECD,添加AC=DC可以利用SAS来进行判定;添加∠B=∠E可以利用ASA来进行判定;添加∠A=∠D可以利用AAS来进行判定.
AC=DC或∠B=∠E或∠A=∠D
【解析】试题分析:本题根据∠BCE=∠CAD可得∠BCA=∠ECD,添加AC=DC可以利用SAS来进行判定;添加∠B=∠E可以利用ASA来进行判定;添加∠A=∠D可以利用AAS来进行判定. 
