题目内容
如图,已知BC=EC,∠BCE=∠ACD,要使△ABC≌△DEC,则应添加的一个条件为 (答案不唯一,只需填一个)
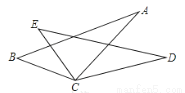
 AC=DC或∠B=∠E或∠A=∠D
【解析】试题分析:本题根据∠BCE=∠CAD可得∠BCA=∠ECD,添加AC=DC可以利用SAS来进行判定;添加∠B=∠E可以利用ASA来进行判定;添加∠A=∠D可以利用AAS来进行判定.
AC=DC或∠B=∠E或∠A=∠D
【解析】试题分析:本题根据∠BCE=∠CAD可得∠BCA=∠ECD,添加AC=DC可以利用SAS来进行判定;添加∠B=∠E可以利用ASA来进行判定;添加∠A=∠D可以利用AAS来进行判定.
练习册系列答案
相关题目
已知x=2是不等式(x-5)(ax-3a+2)≤0的解,且x=1不是这个不等式的解,则实数a的取值范围是( )
A. a>1 B. a≤2 C. 1<a≤2 D. 1≤a≤2
 C
【解析】根据x=2是不等式(x-5)(ax-3a+2)≤0的解,可知(2-5)(2a-3a+2)≤0,解得:a≤2,再根据x=1不是这个不等式的解,可得(1-5)(a-3a+2)>0,解得:a>1,
由此可得a的取值范围为:1<a≤2.
故选:C.
C
【解析】根据x=2是不等式(x-5)(ax-3a+2)≤0的解,可知(2-5)(2a-3a+2)≤0,解得:a≤2,再根据x=1不是这个不等式的解,可得(1-5)(a-3a+2)>0,解得:a>1,
由此可得a的取值范围为:1<a≤2.
故选:C. 如果多项式x2-kx+9能用公式法分解因式,则k的值是多少?
 k=±6
【解析】试题分析:根据题意判断出题目中的多项式为完全平方式,然后可根据完全平方式计算即可.
试题解析:∵多项式x2-kx+9能用公式法分解因式,并且它有三项,
∴它是一个完全平方式,
∴这两个数是3、x,
∴k=±2×3=±6
k=±6
【解析】试题分析:根据题意判断出题目中的多项式为完全平方式,然后可根据完全平方式计算即可.
试题解析:∵多项式x2-kx+9能用公式法分解因式,并且它有三项,
∴它是一个完全平方式,
∴这两个数是3、x,
∴k=±2×3=±6 如果多项式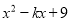 能用公式法分解因式,那么k的值是( )
能用公式法分解因式,那么k的值是( )
A. 3 B. 6 C. 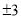 D.
D. 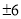
 D
【解析】由于可以利用公式法分解因式,所以它是一个完全平方式,所以.
故选:D.
D
【解析】由于可以利用公式法分解因式,所以它是一个完全平方式,所以.
故选:D. 如图,已知AB=AC,E,D分别是AB,AC的中点,且AF⊥BD交BD的延长线于F,AG⊥CE交CE的延长线于G,试判断AF和AG的关系是否相等,并说明理由.
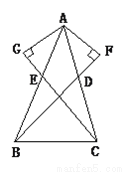
 AF=AG
【解析】试题分析:先由SAS证得△ABD≌△ACE,由全等三角形对应边相等得∠ABD=∠ACE,由AAS证得△ABF≌△ACG,即可证得AF=AG.
试题解析:
∵AB=AC,E,D分别是AB,AC的中点,
∴ AD=AE.
∴在△ABD和△ACE中,
∴△ABD≌△ACE (SAS).
∴∠ABD=∠ACE,
在△ABF和△ACG中,
...
AF=AG
【解析】试题分析:先由SAS证得△ABD≌△ACE,由全等三角形对应边相等得∠ABD=∠ACE,由AAS证得△ABF≌△ACG,即可证得AF=AG.
试题解析:
∵AB=AC,E,D分别是AB,AC的中点,
∴ AD=AE.
∴在△ABD和△ACE中,
∴△ABD≌△ACE (SAS).
∴∠ABD=∠ACE,
在△ABF和△ACG中,
... 如图,AC=AD,BC=BD,则有( )
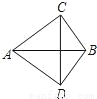
A. AB垂直平分CD B. CD垂直平分AB
C. AB与CD互相垂直平分 D. CD平分∠ACB
 A
【解析】试题分析:因为AC=AD,BC=BD,所以点A和点B在线段CD的垂直平分线上,即AB垂直平分CD,故选;A.
A
【解析】试题分析:因为AC=AD,BC=BD,所以点A和点B在线段CD的垂直平分线上,即AB垂直平分CD,故选;A. 在下列条件中,不能说明△ABC≌△A’B’C’的是( )
A. ∠A=∠A’,∠C=∠C’,AC=A’C’ B. ∠A=∠A’,AB=A’B’,BC=B’C’
C. ∠B=∠B’,∠C=∠C’,AB=A’B’ D. AB=A’B’, BC=B’ C’AC=A’C’
 B
【解析】A、∠A=∠A′,∠C=∠C′,AC=A′C′,可用ASA判定△ABC≌△A′B′C,故选项正确;
B、∠A=∠A′,AB=A′B′,BC=B′C′,SSA不能判定两个三角形全等,故选项错误;
C、∠B=∠B′,∠C=∠C′,AB=A′B′,可用AAS判定△ABC≌△A′B′C,故选项正确;
D、AB=A′B′,BC=B′C,AC=A′C′,可用ASA判定△AB...
B
【解析】A、∠A=∠A′,∠C=∠C′,AC=A′C′,可用ASA判定△ABC≌△A′B′C,故选项正确;
B、∠A=∠A′,AB=A′B′,BC=B′C′,SSA不能判定两个三角形全等,故选项错误;
C、∠B=∠B′,∠C=∠C′,AB=A′B′,可用AAS判定△ABC≌△A′B′C,故选项正确;
D、AB=A′B′,BC=B′C,AC=A′C′,可用ASA判定△AB... 当x=_____时,分式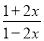 的值为零.
的值为零.
 【解析】由题意可得1+2x=0且1-2x≠0,解得x=.
故当x=时,分式的值为零。故答案为: .
【解析】由题意可得1+2x=0且1-2x≠0,解得x=.
故当x=时,分式的值为零。故答案为: . 已知:△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点.求证:四边形DEFG是平行四边形.
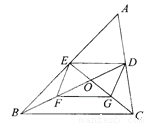
 证明见解析.
【解析】试题分析:根据BD,CE是△ABC的中线可得DE是△ABC的中位线,F,G分别是OB,OC的中点可得FG是△BOC的中位线,根据三角形中位线定理可得DE∥BC且DE=BC,FG∥BC且FG=BC,进而可得DE∥FG且DE=FG,根据一组对边平行且相等的四边形是平行四边形可得结论.
试题解析:∵BD、CE是△ABC的中线,∴DE是△ABC的中位线,
∴DE∥B...
证明见解析.
【解析】试题分析:根据BD,CE是△ABC的中线可得DE是△ABC的中位线,F,G分别是OB,OC的中点可得FG是△BOC的中位线,根据三角形中位线定理可得DE∥BC且DE=BC,FG∥BC且FG=BC,进而可得DE∥FG且DE=FG,根据一组对边平行且相等的四边形是平行四边形可得结论.
试题解析:∵BD、CE是△ABC的中线,∴DE是△ABC的中位线,
∴DE∥B... 
