��Ŀ����
�������ⲻ��ȷ���ǣ�������
A. �����ڽǷֱ���50���65����������ǵ���������
B. ���������ȵ��������ǵ���������
C. һ����ǵ�ƽ����ƽ����һ�ߵ��������ǵ���������
D. �����ڽDz���ȵ������β��ǵ���������
 D
���������⣺A����������180�㩁50�㩁65��=65�㣬��������ȵ��������ǵ��������Σ���ȷ��
B�������ȣ����Ӧ���ڽ�Ҳ��ȣ���������ȵ��������ǵ��������Σ���ȷ��
C��������ֱ��ƽ�У��ڴ�����ȣ�ͬλ��ȣ���֪����������ڽ�Ҳ��ȣ���������ȵ��������ǵ��������Σ���ȷ��
D�������ڽDz���ȵ������ο����ǵ��������Σ�����
��ѡD��
D
���������⣺A����������180�㩁50�㩁65��=65�㣬��������ȵ��������ǵ��������Σ���ȷ��
B�������ȣ����Ӧ���ڽ�Ҳ��ȣ���������ȵ��������ǵ��������Σ���ȷ��
C��������ֱ��ƽ�У��ڴ�����ȣ�ͬλ��ȣ���֪����������ڽ�Ҳ��ȣ���������ȵ��������ǵ��������Σ���ȷ��
D�������ڽDz���ȵ������ο����ǵ��������Σ�����
��ѡD��
��ͼ��ʾ��DΪ��ABC�ı�AB���ӳ�����һ�㣬��D��DF��AC������ΪF����BC��E,��BD=BE,��֤����ABC�ǵ���������.
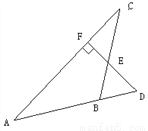
 ֤��������
������������������������Ʒ�����֤��ABC�ǵ��������Σ���ͼ��֪Ӧ֤AB=BC���ɡ��ȽǶԵȱߡ���Ӧ�뵽ֻҪ֤��A=��C���ɽǵĻ����ϵ��֪��A����D=90�㣬��C����CEF=90�㣬��CEF =��BED����BD=BE��֪��BED=��D���ɵá�A=��C�������֤��
�����������BD��BE�����BDE����BED��
�֡ߡ�BED����CEF�����BDE����CEF��
��...
֤��������
������������������������Ʒ�����֤��ABC�ǵ��������Σ���ͼ��֪Ӧ֤AB=BC���ɡ��ȽǶԵȱߡ���Ӧ�뵽ֻҪ֤��A=��C���ɽǵĻ����ϵ��֪��A����D=90�㣬��C����CEF=90�㣬��CEF =��BED����BD=BE��֪��BED=��D���ɵá�A=��C�������֤��
�����������BD��BE�����BDE����BED��
�֡ߡ�BED����CEF�����BDE����CEF��
��... ij��ѧ������������ϰ����ҵ�Ͻ�һ��һԪһ�β���ʽʱ�����ֲ���ʽ�ұߵ�һ������ī����Ⱦ�������ˣ��������IJ���ʽ��1��3x���~�����鿴��ϰ����Ĵ�֪�����������ʽ�Ľ⼯��x��5����ô����Ⱦ������ __________ ��
 ��14
���������豻��Ⱦ����Ϊa������ʽΪ1-3x��a����ã�x��������֪�⼯Ϊx��5���õ�=5��ã�a=-14.
�ʴ�Ϊ��-14
��14
���������豻��Ⱦ����Ϊa������ʽΪ1-3x��a����ã�x��������֪�⼯Ϊx��5���õ�=5��ã�a=-14.
�ʴ�Ϊ��-14 ��֪x=2�Dz���ʽ��x-5����ax-3a+2����0�Ľ⣬��x=1�����������ʽ�Ľ⣬��ʵ��a��ȡֵ��Χ�ǣ� ��
A. a��1 B. a��2 C. 1��a��2 D. 1��a��2
 C
������������x=2�Dz���ʽ��x-5����ax-3a+2����0�Ľ⣬��֪��2-5����2a-3a+2����0����ã�a��2���ٸ���x=1�����������ʽ�Ľ⣬�ɵã�1-5����a-3a+2����0����ã�a��1��
�ɴ˿ɵ�a��ȡֵ��ΧΪ��1��a��2��
��ѡ��C.
C
������������x=2�Dz���ʽ��x-5����ax-3a+2����0�Ľ⣬��֪��2-5����2a-3a+2����0����ã�a��2���ٸ���x=1�����������ʽ�Ľ⣬�ɵã�1-5����a-3a+2����0����ã�a��1��
�ɴ˿ɵ�a��ȡֵ��ΧΪ��1��a��2��
��ѡ��C. ��ͼ,һ�Һ���λ�ڵ���P��ƫ��70�㷽���M��,����ÿʱ40������ٶ�������������,2ʱ��λ�ڵ���P��ƫ��40�㷽���N��,��N�������P�ľ���Ϊ(����)
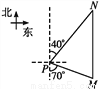
A. 40���� B. 60����
C. 70���� D. 80����
 D
�����������������MN=2��40=80�������
�ߡ�M=70�㣬��N=40�㣬
���NPM=180��-��M-��N=180��-70��-40��=70�㣬
���NPM=��M��
��NP=MN=80�������
��ѡD��
D
�����������������MN=2��40=80�������
�ߡ�M=70�㣬��N=40�㣬
���NPM=180��-��M-��N=180��-70��-40��=70�㣬
���NPM=��M��
��NP=MN=80�������
��ѡD�� 19992+1999�ܱ�2000������
 ��
����������������������ṫ��ʽ��--��ʽ�ֽ⣬��Ϊ��������������ʽ�����õ������Ľ���.
�����������Ϊ19992+1999=1999����1999+1��=1999��2000��
����19992+1999�ܱ�1999������Ҳ�ܱ�2000����.
��
����������������������ṫ��ʽ��--��ʽ�ֽ⣬��Ϊ��������������ʽ�����õ������Ľ���.
�����������Ϊ19992+1999=1999����1999+1��=1999��2000��
����19992+1999�ܱ�1999������Ҳ�ܱ�2000����. ______
 ��������������ʽ�˷�����ʽ�ֽ�Ļ����ԣ���֪3x��x+1��=3x2+x.
�ʴ�Ϊ��3x2+x.
��������������ʽ�˷�����ʽ�ֽ�Ļ����ԣ���֪3x��x+1��=3x2+x.
�ʴ�Ϊ��3x2+x. �������ʽx2-kx+9���ù�ʽ���ֽ���ʽ����k��ֵ�Ƕ��٣�
 k=��6
��������������������������жϳ���Ŀ�еĶ���ʽΪ��ȫƽ��ʽ��Ȼ��ɸ�����ȫƽ��ʽ���㼴��.
����������߶���ʽx2-kx+9���ù�ʽ���ֽ���ʽ�������������
������һ����ȫƽ��ʽ��
������������3��x��
��k=��2��3=��6
k=��6
��������������������������жϳ���Ŀ�еĶ���ʽΪ��ȫƽ��ʽ��Ȼ��ɸ�����ȫƽ��ʽ���㼴��.
����������߶���ʽx2-kx+9���ù�ʽ���ֽ���ʽ�������������
������һ����ȫƽ��ʽ��
������������3��x��
��k=��2��3=��6 �����������У�����˵����ABC�ա�A��B��C������( )
A. ��A����A������C����C����AC��A��C�� B. ��A����A����AB��A��B����BC��B��C��
C. ��B����B������C����C����AB��A��B�� D. AB��A��B���� BC��B�� C��AC��A��C��
 B
��������A����A=��A�䣬��C=��C�䣬AC=A��C�䣬����ASA�ж���ABC�ա�A��B��C����ѡ����ȷ��
B����A=��A�䣬AB=A��B�䣬BC=B��C�䣬SSA�����ж�����������ȫ�ȣ���ѡ�����
C����B=��B�䣬��C=��C�䣬AB=A��B�䣬����AAS�ж���ABC�ա�A��B��C����ѡ����ȷ��
D��AB=A��B�䣬BC=B��C��AC=A��C�䣬����ASA�ж���AB...
B
��������A����A=��A�䣬��C=��C�䣬AC=A��C�䣬����ASA�ж���ABC�ա�A��B��C����ѡ����ȷ��
B����A=��A�䣬AB=A��B�䣬BC=B��C�䣬SSA�����ж�����������ȫ�ȣ���ѡ�����
C����B=��B�䣬��C=��C�䣬AB=A��B�䣬����AAS�ж���ABC�ա�A��B��C����ѡ����ȷ��
D��AB=A��B�䣬BC=B��C��AC=A��C�䣬����ASA�ж���AB... 
