题目内容
设a，b，c，d都是整数，且a＜2b，b＜3c，c＜4d，d＜20，则a的最大值是（ ）
A. 480 B. 479 C. 448 D. 447
D
【解析】由a，b，c，d都是整数，且a＜2b，b＜3c，c＜4d，d＜20，可知d=19，c＜4×19=76，代入可得c=75，b＜3×75=225，再次代入b=224，a＜2×224=448，因此可求出a=447，
故选：D．
练习册系列答案
相关题目
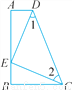
如图，∠A＝∠B＝90°，E是AB上一点，且AE＝BC，∠1＝∠2.求证：△ADE≌△BEC.
证明见解析
【解析】试题分析：由∠1=∠2，可得DE=CD，根据证明直角三角形全等的“HL”定理，证明即可.
试题解析：∵∠1＝∠2，
∴DE＝EC.
又∵∠A＝∠B＝90°，AE＝BC，
∴Rt△ADE≌Rt△BEC(HL). 图形平移的主要因素是移动的________________
方向和距离
【解析】试题解析：图形的平移主要有两个方面决定即方向和距离.
故答案为：方向和距离. 将长度为5cm的线段向上平移10cm所得线段长度是（ ）
A. 10cm B. 5cm C. 0cm D. 无法确定
B
【解析】平移不改变图形的大小和形状．故线段长度不变，仍为5cm． 某中学初中生在做练习册作业上解一个一元一次不等式时，发现不等式右边的一个数被墨迹污染看不清了，所看到的不等式是1－3x＜▇，他查看练习本后的答案知道，这个不等式的解集是x＞5，那么被污染的数是 __________ ．
－14
【解析】设被污染的数为a，不等式为1-3x＜a，解得：x＞，由已知解集为x＞5，得到=5解得：a=-14.
故答案为：-14 已知x=2是不等式（x-5）（ax-3a+2）≤0的解，且x=1不是这个不等式的解，则实数a的取值范围是（ ）
A. a＞1 B. a≤2 C. 1＜a≤2 D. 1≤a≤2
C
【解析】根据x=2是不等式（x-5）（ax-3a+2）≤0的解，可知（2-5）（2a-3a+2）≤0，解得：a≤2，再根据x=1不是这个不等式的解，可得（1-5）（a-3a+2）＞0，解得：a＞1，
由此可得a的取值范围为：1＜a≤2．
故选：C. 已知x=2是不等式（x-5）（ax-3a+2）≤0的解，且x=1不是这个不等式的解，则实数a的取值范围是（ ）
A. a＞1 B. a≤2 C. 1＜a≤2 D. 1≤a≤2
C
【解析】根据x=2是不等式（x-5）（ax-3a+2）≤0的解，可知（2-5）（2a-3a+2）≤0，解得：a≤2，再根据x=1不是这个不等式的解，可得（1-5）（a-3a+2）＞0，解得：a＞1，
由此可得a的取值范围为：1＜a≤2．
故选：C. 19992+1999能被2000整除吗？
能
【解析】试题分析：根据提公因式法--因式分解，化为几个因数积的形式，而得到整除的结论.
试题解析：因为19992+1999=1999×（1999+1）=1999×2000，
所以19992+1999能被1999整除，也能被2000整除. 如果多项式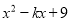
能用公式法分解因式，那么k的值是（ ）
A. 3 B. 6 C.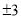 
D. 
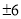
D
【解析】由于可以利用公式法分解因式，所以它是一个完全平方式，所以.
故选：D.