题目内容
如图,在△ABC中,∠B与∠C的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E.若AB=5,AC=4,则△ADE的周长是__________.
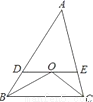
 9
【解析】∵在△ABC中,∠B与∠C的平分线交于点O,
∴∠DBO=∠CBO,∠ECO=∠BCO,
∵DE∥BC,
∴∠DOB=∠CBO,∠EOC=∠BCO,
∴∠DBO=∠DOB,∠ECO=∠EOC,
∴OD=BD,OE=CE,
∵AB=5,AC=4,
∴△ADE的周长为:AD+DE+AE=AD+DO+EO+AE=AD+DB+EC+AE=AB+A...
9
【解析】∵在△ABC中,∠B与∠C的平分线交于点O,
∴∠DBO=∠CBO,∠ECO=∠BCO,
∵DE∥BC,
∴∠DOB=∠CBO,∠EOC=∠BCO,
∴∠DBO=∠DOB,∠ECO=∠EOC,
∴OD=BD,OE=CE,
∵AB=5,AC=4,
∴△ADE的周长为:AD+DE+AE=AD+DO+EO+AE=AD+DB+EC+AE=AB+A...
练习册系列答案
相关题目
下列可使两个直角三角形全等的条件是( )
A. 一条边对应相等 B. 两条直角边对应相等
C. 一个锐角对应相等 D. 两个锐角对应相等
 B
【解析】【解析】
两直角三角形隐含一个条件是两直角相等,要判定两直角三角形全等,起码还要两个条件,故可排除A、C;
而D构成了AAA,不能判定全等;
B构成了SAS,可以判定两个直角三角形全等.
故选B.
B
【解析】【解析】
两直角三角形隐含一个条件是两直角相等,要判定两直角三角形全等,起码还要两个条件,故可排除A、C;
而D构成了AAA,不能判定全等;
B构成了SAS,可以判定两个直角三角形全等.
故选B. 将长度为5cm的线段向上平移10cm所得线段长度是( )
A. 10cm B. 5cm C. 0cm D. 无法确定
 B
【解析】平移不改变图形的大小和形状.故线段长度不变,仍为5cm.
B
【解析】平移不改变图形的大小和形状.故线段长度不变,仍为5cm. 已知x=2是不等式(x-5)(ax-3a+2)≤0的解,且x=1不是这个不等式的解,则实数a的取值范围是( )
A. a>1 B. a≤2 C. 1<a≤2 D. 1≤a≤2
 C
【解析】根据x=2是不等式(x-5)(ax-3a+2)≤0的解,可知(2-5)(2a-3a+2)≤0,解得:a≤2,再根据x=1不是这个不等式的解,可得(1-5)(a-3a+2)>0,解得:a>1,
由此可得a的取值范围为:1<a≤2.
故选:C.
C
【解析】根据x=2是不等式(x-5)(ax-3a+2)≤0的解,可知(2-5)(2a-3a+2)≤0,解得:a≤2,再根据x=1不是这个不等式的解,可得(1-5)(a-3a+2)>0,解得:a>1,
由此可得a的取值范围为:1<a≤2.
故选:C. 已知x=2是不等式(x-5)(ax-3a+2)≤0的解,且x=1不是这个不等式的解,则实数a的取值范围是( )
A. a>1 B. a≤2 C. 1<a≤2 D. 1≤a≤2
 C
【解析】根据x=2是不等式(x-5)(ax-3a+2)≤0的解,可知(2-5)(2a-3a+2)≤0,解得:a≤2,再根据x=1不是这个不等式的解,可得(1-5)(a-3a+2)>0,解得:a>1,
由此可得a的取值范围为:1<a≤2.
故选:C.
C
【解析】根据x=2是不等式(x-5)(ax-3a+2)≤0的解,可知(2-5)(2a-3a+2)≤0,解得:a≤2,再根据x=1不是这个不等式的解,可得(1-5)(a-3a+2)>0,解得:a>1,
由此可得a的取值范围为:1<a≤2.
故选:C. 用反证法证明“三角形中至少有一个内角不小于60°”,应先假设这个三角形中( )
A. 有一个内角小于60° B. 每一个内角都小于60°
C. 有一个内角大于60° D. 每一个内角都大于60°
 B
【解析】试题分析:此题要运用反证法,由题意先假设三角形的三个角都小于60°成立.然后推出不成立.得出选项.
【解析】
设三角形的三个角分别为:a,b,c.
假设,a<60°,b<60°,c<60°,
则a+b+c<60°+60°+60°,
即,a+b+c<180°与三角形内角和定理a+b+c=180°矛盾.
所以假设不成立,即三角形中至少有一个角不小于60...
B
【解析】试题分析:此题要运用反证法,由题意先假设三角形的三个角都小于60°成立.然后推出不成立.得出选项.
【解析】
设三角形的三个角分别为:a,b,c.
假设,a<60°,b<60°,c<60°,
则a+b+c<60°+60°+60°,
即,a+b+c<180°与三角形内角和定理a+b+c=180°矛盾.
所以假设不成立,即三角形中至少有一个角不小于60... 19992+1999能被2000整除吗?
 能
【解析】试题分析:根据提公因式法--因式分解,化为几个因数积的形式,而得到整除的结论.
试题解析:因为19992+1999=1999×(1999+1)=1999×2000,
所以19992+1999能被1999整除,也能被2000整除.
能
【解析】试题分析:根据提公因式法--因式分解,化为几个因数积的形式,而得到整除的结论.
试题解析:因为19992+1999=1999×(1999+1)=1999×2000,
所以19992+1999能被1999整除,也能被2000整除. 一个多项式分解因式的结果是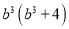 ,那么这个多项式是( )
,那么这个多项式是( )
A. 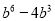 B.
B. 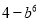 C.
C. 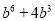 D.
D. 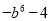
 C
【解析】利用因式分解是整式乘法的逆运算,可知=.
故选:C.
C
【解析】利用因式分解是整式乘法的逆运算,可知=.
故选:C. 如图,AC=AD,BC=BD,则有( )
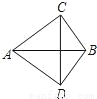
A. AB垂直平分CD B. CD垂直平分AB
C. AB与CD互相垂直平分 D. CD平分∠ACB
 A
【解析】试题分析:因为AC=AD,BC=BD,所以点A和点B在线段CD的垂直平分线上,即AB垂直平分CD,故选;A.
A
【解析】试题分析:因为AC=AD,BC=BD,所以点A和点B在线段CD的垂直平分线上,即AB垂直平分CD,故选;A. 
