题目内容
4. 如图,点D是△ABC的边BC上一点,且BD:CD=2:3,点E,F分别是线段AD,CE的中点,且△ABC的面积为20cm2.
如图,点D是△ABC的边BC上一点,且BD:CD=2:3,点E,F分别是线段AD,CE的中点,且△ABC的面积为20cm2.(1)求△CDE的面积;
(2)求△BEF的面积.
分析 (1)根据等高的三角形面积的比等于底的比求得三角形ADC的面积和三角形ABD的面积,然后根据三角形的中线把三角形分成两个面积相等的三角形即可求得△CDE的面积;
(2)求得三角形BCE的面积,然后根据三角形的中线把三角形分成两个面积相等的三角形即可求得△BEF的面积.
解答 解:(1)∵△ABD和△ADC不等底等高,BD:CD=2:3,
∴S△ABD=$\frac{2}{5}$S△ABC=8,S△ADC=20-8=12,
∵点E是AD的中点,
∴S△CDE=$\frac{1}{2}$S△ADC=$\frac{1}{2}$×12=6(cm2);
(2)∵S△BDE=$\frac{1}{2}$S△ABD=$\frac{1}{2}$×8=4
∴S△BCE=S△BDE+S△DCE=6+4=10,
∵点F是CE的中点,
∴S△BEF=$\frac{1}{2}$S△BCE=$\frac{1}{2}$×10=5(cm2).
点评 本题考查了三角形的面积,主要利用了三角形的中线把三角形分成两个面积相等的三角形,原理为等底等高的三角形的面积相等.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
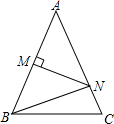 如图,△ABC中,AB=AC,∠A=38°,MN垂直平分AB,则∠BNC=76°.
如图,△ABC中,AB=AC,∠A=38°,MN垂直平分AB,则∠BNC=76°.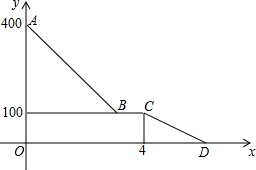 小红驾车从甲地到乙地,设她出发第xh时距离乙地ykm,图中的折线表示她在整个驾车过程中y与x之间的函数关系.
小红驾车从甲地到乙地,设她出发第xh时距离乙地ykm,图中的折线表示她在整个驾车过程中y与x之间的函数关系.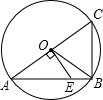 如图,AC是⊙O的直径,OE⊥AC交弦AB于E,若BC=4,S△AOE=5,则sin∠BOE的值为$\frac{3}{5}$.
如图,AC是⊙O的直径,OE⊥AC交弦AB于E,若BC=4,S△AOE=5,则sin∠BOE的值为$\frac{3}{5}$.