题目内容
14.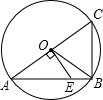 如图,AC是⊙O的直径,OE⊥AC交弦AB于E,若BC=4,S△AOE=5,则sin∠BOE的值为$\frac{3}{5}$.
如图,AC是⊙O的直径,OE⊥AC交弦AB于E,若BC=4,S△AOE=5,则sin∠BOE的值为$\frac{3}{5}$.
分析 由题意可知,OE为直径AC的中垂线,则CE=AE=5,S△AEC=2S△AOE=10,由S△AEC求出线段AE的长度,进而在Rt△BCE中,由勾股定理求出线段BE的长度;然后证明∠BOE=∠BCE,从而可求得结果.
解答 如图,连接EC.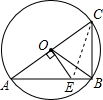
由题意可得,OE为直径AC的垂直平分线,∠ABC=90°,
∴CE=AE,S△AOE=S△COE=5,
∴S△AEC=2S△AOE=10.
∴$\frac{1}{2}$AE•BC=10,
∵BC=4,
∴AE=5,
∴EC=5.
在Rt△BCE中,由勾股定理得:BE=$\sqrt{C{E}^{2}-B{C}^{2}}$=3.
∵∠EBC+∠EOC=90°+90°=180°,
∴B、C、O、E四点共圆,
∴∠BOE=∠BCE.
∴sin∠BOE=sin∠BCE=$\frac{3}{5}$.
故答案为:$\frac{3}{5}$.
点评 此题考查了线段垂直平分线的性质;勾股定理;圆周角定理;锐角三角函数的定义.解题的关键是:添加辅助线将∠BOE转化为∠BCE.

练习册系列答案
相关题目
 如图,点D是△ABC的边BC上一点,且BD:CD=2:3,点E,F分别是线段AD,CE的中点,且△ABC的面积为20cm2.
如图,点D是△ABC的边BC上一点,且BD:CD=2:3,点E,F分别是线段AD,CE的中点,且△ABC的面积为20cm2.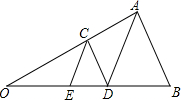 已知,如图,在△AOB中,点C在OA上,点E、D在OB上,且AB=AD,CD∥AB,CE∥AD,问:△CDE是否为等腰三角形?为什么?
已知,如图,在△AOB中,点C在OA上,点E、D在OB上,且AB=AD,CD∥AB,CE∥AD,问:△CDE是否为等腰三角形?为什么?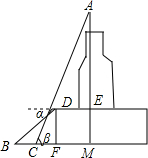 如图所示为某大厦的示意图其中裙楼共有10层,现测得DF的高为55米,吴莉在D处测得地面上点B的俯角α为30°,点D到AM的距离DE为60米,从地面上的点B沿BM方向走到点C处,测得BC=50米,大厦顶尖A的仰角β为65°,请根据以上测量数据计算大厦的高AM.(结果精确到0.1米,参考数据:sin65°≈0.906,cos65°≈0.423,tan65°≈2.143,$\sqrt{3}$≈1.732)
如图所示为某大厦的示意图其中裙楼共有10层,现测得DF的高为55米,吴莉在D处测得地面上点B的俯角α为30°,点D到AM的距离DE为60米,从地面上的点B沿BM方向走到点C处,测得BC=50米,大厦顶尖A的仰角β为65°,请根据以上测量数据计算大厦的高AM.(结果精确到0.1米,参考数据:sin65°≈0.906,cos65°≈0.423,tan65°≈2.143,$\sqrt{3}$≈1.732)