题目内容
15.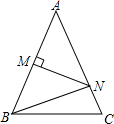 如图,△ABC中,AB=AC,∠A=38°,MN垂直平分AB,则∠BNC=76°.
如图,△ABC中,AB=AC,∠A=38°,MN垂直平分AB,则∠BNC=76°.
分析 先由线段垂直平分线的性质可得AN=BN,然后根据等边对等角,可得:∠A=∠ABN=38°,然后根据三角形外角的性质可得∠BNC=∠A+∠ABN=76°.
解答 解:∵MN垂直平分AB,
∴AN=BN,
∴∠A=∠ABN=38°,
∵∠BNC是△ABN的外角,
∴∠BNC=∠A+∠ABN=76°,
故答案为:76°.
点评 本题考查线段垂直平分线的性质及三角形外角的性质.由题中MN是线段AB的垂直平分线这一条件时,一般要用到它的性质定理:线段垂直平分线上的点到线段两端的距离相等.从而结合图形找到这对相等的线段是解决问题的关键.

练习册系列答案
相关题目
5.下列四个多项式,能因式分解的是( )
| A. | a-1 | B. | a2+1 | C. | x2-4y | D. | x2-6x+9 |
10.边长为2的等边三角形的高为( )
| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
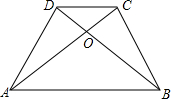 如图,已知在梯形ABCD中,AB∥CD,且AB=3CD,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,那么$\overrightarrow{AO}$$\frac{1}{4}\overrightarrow{a}$+$\frac{3}{4}\overrightarrow{b}$(用$\overrightarrow{a}$,$\overrightarrow{b}$的式子表示)
如图,已知在梯形ABCD中,AB∥CD,且AB=3CD,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,那么$\overrightarrow{AO}$$\frac{1}{4}\overrightarrow{a}$+$\frac{3}{4}\overrightarrow{b}$(用$\overrightarrow{a}$,$\overrightarrow{b}$的式子表示) 如图,将正整数按如图所示规律排列下去,若用有序数对(m,n)表示m排从左到右第n个数.如(4,3)表示9,则(15,4)表示109.
如图,将正整数按如图所示规律排列下去,若用有序数对(m,n)表示m排从左到右第n个数.如(4,3)表示9,则(15,4)表示109. 如图,在正方形ABCD中,E、F分别是边BC、CD上的点,∠EAF=45°,正方形ABCD的边长为3,则△ECF的周长为6.
如图,在正方形ABCD中,E、F分别是边BC、CD上的点,∠EAF=45°,正方形ABCD的边长为3,则△ECF的周长为6. 如图,点D是△ABC的边BC上一点,且BD:CD=2:3,点E,F分别是线段AD,CE的中点,且△ABC的面积为20cm2.
如图,点D是△ABC的边BC上一点,且BD:CD=2:3,点E,F分别是线段AD,CE的中点,且△ABC的面积为20cm2.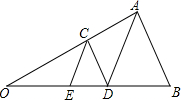 已知,如图,在△AOB中,点C在OA上,点E、D在OB上,且AB=AD,CD∥AB,CE∥AD,问:△CDE是否为等腰三角形?为什么?
已知,如图,在△AOB中,点C在OA上,点E、D在OB上,且AB=AD,CD∥AB,CE∥AD,问:△CDE是否为等腰三角形?为什么?