题目内容

8．化简：$\frac{2x}{{x}^{2}-4{y}^{2}}$÷（1+$\frac{x-2y}{x+2y}$）

分析 原式括号中两项通分并利用同分母分式的加法法则计算，同时利用除法法则变形，约分即可得到结果．

解答 解；原式=$\frac{2x}{（x+2y）（x-2y）}$•$\frac{x+2y}{2x}$=$\frac{1}{x-2y}$．

点评 此题考查了分式的混合运算，熟练掌握运算法则是解本题的关键．

练习册系列答案
相关题目
18．随着襄阳市近几年城市建设的快速发展，对花木的需求量逐年提高．某园林专业户计划投资种植花卉及树木，根据市场调查与预测，种植树木的利润y1与投资量x成正比例关系，如图1所示；种植花卉的利润y2与投资量x成二次函数关系，如图2所示（注：利润与投资量的单位：万元）
（1）分别求出利润y1与y2关于投资量x的函数关系式；
（2）如果这位专业户以10万元资金投入种植花卉和树木，求他获得的最大利润是多少？
（3）在（2）的条件下，根据对市场需求的调查，这位专业户决定投入种植树木的资金不得高于投入种植花卉的资金，他至少获得多少利润？
19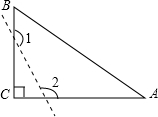．如图，已知△ABC中，∠C=90°，若沿图中虚线剪去∠C，则∠1+∠2等于（　　）
A．90°B．135°C．270°D．315°
16．方程2x（x-3）=5（x-3）的根为（　　）
A．x=$\frac{5}{2}$，x=3B．x=3C．x=-3D．x=$\frac{2}{5}$，x=3
3．有这样一类题目：将$\sqrt{a±2\sqrt{b}}$化简，如果你能找到两个数m、n，使m2+n2=a且mn=$\sqrt{b}$，则可将a±2$\sqrt{b}$将变成m2+n2±2mn，即变成（m+n）2，从而使得$\sqrt{a±2\sqrt{b}}$化简．例如，5±2$\sqrt{6}$=3+2±2$\sqrt{6}$=（$\sqrt{3}$）2+（$\sqrt{2}$）2±2$\sqrt{2}$×$\sqrt{3}$=（$\sqrt{3}$±$\sqrt{2}$）2，∴$\sqrt{5±2\sqrt{6}}$=$\sqrt{（\sqrt{3}±\sqrt{2}）}$2=（$\sqrt{3}$±$\sqrt{2}$）．这种方法叫做配方法，换一种思路，假设化简5±2$\sqrt{6}$的结果是$\sqrt{x}$±$\sqrt{y}$（x＞y＞0），可知5±2$\sqrt{6}$=（$\sqrt{x}$±$\sqrt{y}$）2．整理，得5±2$\sqrt{6}$=x+y±2$\sqrt{xy}$，比较等式两边的组成，可得x+y=5，xy=6，即x=3，y=2，所以$\sqrt{5±2\sqrt{6}}$=（$\sqrt{3}$±$\sqrt{2}$）．
尝试化简下列各式：
（1）$\sqrt{7+4\sqrt{3}}$；
（2）$\sqrt{8-\sqrt{60}}$．
13．不能判定一个四边形是平行四边形的条件是（　　）
A．两组对边分别平行B．一组对边平行且相等
C．一组对边平行，另一组对边相等D．两组对边分别相等
20．从1到48这48个数中随机选取一个数，选出的数是2或3的倍数但不是6的倍数的概率是$\frac{1}{2}$．
17．解下列方程组：
（1）$\left\{\begin{array}{l}{3x-y+z=3}\\{2x+y-3z=11}\\{x+y+z=12}\end{array}\right.$
（2）$\left\{\begin{array}{l}{5x-4y+4z=13}\\{2x+7y-3z=19}\\{3x+2y-z=18}\end{array}\right.$．
18．某一次函数的函数关系为kx+（k+1）y=1（k是正整数），当k=1时，函数图象与两坐标轴所围成图形的面积为S1，当k=2时，面积为S2，…，当k=n时，面积为Sn，则S1+S2+…+Sn=$\frac{n}{2n+2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网