题目内容
17.解下列方程组:(1)$\left\{\begin{array}{l}{3x-y+z=3}\\{2x+y-3z=11}\\{x+y+z=12}\end{array}\right.$
(2)$\left\{\begin{array}{l}{5x-4y+4z=13}\\{2x+7y-3z=19}\\{3x+2y-z=18}\end{array}\right.$.
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{3x-y+z=3①}\\{2x+y-3z=11②}\\{x+y+z=12③}\end{array}\right.$,
①+②得:5x-2z=14④,
①+③得:4x+2z=15⑤,
④+⑤得:9x=29,即x=$\frac{29}{9}$,
把x=$\frac{29}{9}$代入④得:z=$\frac{19}{2}$,
把x=$\frac{29}{9}$,z=$\frac{19}{2}$代入③得:y=-$\frac{13}{18}$,
则方程组的解为$\left\{\begin{array}{l}{x=\frac{29}{9}}\\{y=-\frac{13}{18}}\\{z=\frac{19}{2}}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{5x-4y+4z=13①}\\{2x+7y-3z=19②}\\{3x+2y-z=18③}\end{array}\right.$,
①+③×4得:17x+4y=85④,
①×3+②×4得:23x+16y=115⑤,
④×4-⑤得:45x=225,即x=5,
把x=5代入④得:y=0,
把x=5,y=0代入①得:z=-3,
则方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=0}\\{z=-3}\end{array}\right.$.
点评 此题考查了解三元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
7.为了解本班学生每天零花钱使用情况,张明随机调查了15名同学,结果如下表:
关于这15名同学每天使用的零花钱,下列说法错误的是( )
| 每天使用零花钱(单位:元) | 0 | 1 | 3 | 4 | 5 |
| 人数 | 1 | 3 | 5 | 4 | 2 |
| A. | 众数是3元 | B. | 平均数是2.5元 | C. | 极差是5元 | D. | 中位数是3元 |
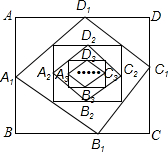 如图所示,已知矩形ABCD,AB=6,BC=8,依次连接矩形ABCD的各边中点构成第一个四边形A1B1C1D1,再依次连接四边形A1B1C1D1的各边中点又得到一个新的四边形A2B2C2D2…,依此类推,当n=2015时,四边形AnBnCnDn的周长为5×($\frac{1}{2}$)2010.
如图所示,已知矩形ABCD,AB=6,BC=8,依次连接矩形ABCD的各边中点构成第一个四边形A1B1C1D1,再依次连接四边形A1B1C1D1的各边中点又得到一个新的四边形A2B2C2D2…,依此类推,当n=2015时,四边形AnBnCnDn的周长为5×($\frac{1}{2}$)2010. 如图所示,在△ABC中,AD⊥BC,AE平分∠BAC,说说为什么∠DAE=$\frac{1}{2}$(∠C-∠B),写出你的推理过程.
如图所示,在△ABC中,AD⊥BC,AE平分∠BAC,说说为什么∠DAE=$\frac{1}{2}$(∠C-∠B),写出你的推理过程.