Question

13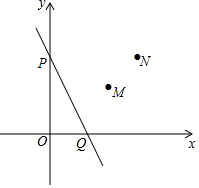．如图，直线l：y=-2x+b与两轴交于点P和点Q，点M（3，2），N（4，4）是第一象限内的两点
（1）当直线l经过M点时，求b的值；
（2）若点M，N位于l的异侧，确定b的取值范围．

Answer 1

分析 （1）将点M的坐标代入一次函数解析式中求出b值即可；
（2）将点N的坐标代入一次函数解析式中求出b值，由直线分别经过点M、N时b的值结合函数图象即可得出若点M，N位于l的异侧，b的取值范围．

解答 解：（1）当直线l经过M点时，有2=-2×3+b，
解得：b=8．
∴当直线l经过M点时，b的值为8．
（2）当直线l经过N点时，有4=-2×4+b，
解得：b=12．
∴若点M，N位于l的异侧，b的取值范围为8＜b＜12．

点评 本题考查了待定系数法求一次函数解析式以及一次函数图象，解题的关键是：（1）根据点M的坐标利用待定系数法求出b值；（2）根据点N的坐标利用待定系数法求出b值．