题目内容
1.已知关于x的方程$\frac{2x+m}{x-2}=5$的解是非负数,则m的取值范围为m≥-10且m≠-4.分析 首先根据解分式方程的方法,求出关于x的方程$\frac{2x+m}{x-2}=5$的解;然后根据关于x的方程$\frac{2x+m}{x-2}=5$的解是非负数,求出m的取值范围即可.
解答 解:∵$\frac{2x+m}{x-2}=5$,
∴x=$\frac{m+10}{3}$,
∵关于x的方程$\frac{2x+m}{x-2}=5$的解是非负数,
∴$\frac{m+10}{3}$≥0,且$\frac{m+10}{3}$≠2,
解得m≥-10且m≠-4,
∴m的取值范围为m≥-10且m≠-4.
故答案为:m≥-10且m≠-4.
点评 此题主要考查了分式方程的解,以及解一元一次不等式的方法,要熟练掌握.

练习册系列答案
相关题目
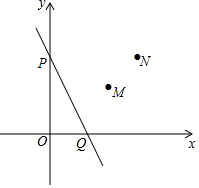 如图,直线l:y=-2x+b与两轴交于点P和点Q,点M(3,2),N(4,4)是第一象限内的两点
如图,直线l:y=-2x+b与两轴交于点P和点Q,点M(3,2),N(4,4)是第一象限内的两点 如图,AB为半圆O的直径,AD、BC分别切⊙O于A,B两点,CD切⊙O于点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2,④OD:OC=DE:OE,⑤OD2=DE•CD,正确的有( )
如图,AB为半圆O的直径,AD、BC分别切⊙O于A,B两点,CD切⊙O于点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2,④OD:OC=DE:OE,⑤OD2=DE•CD,正确的有( )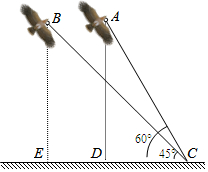 在一个阳光明媚、清风徐来的周末,小明和小强一起到郊外放风筝﹒他们把风筝放飞后,将两个风筝的引线一端都固定在地面上的C处(如图).现已知风筝A的引线(线段AC)长20m,风筝B的引线(线段BC)长24m,在C处测得风筝A的仰角为60°,风筝B的仰角为45°.
在一个阳光明媚、清风徐来的周末,小明和小强一起到郊外放风筝﹒他们把风筝放飞后,将两个风筝的引线一端都固定在地面上的C处(如图).现已知风筝A的引线(线段AC)长20m,风筝B的引线(线段BC)长24m,在C处测得风筝A的仰角为60°,风筝B的仰角为45°.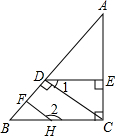 已知,如图,AC⊥BC,HF⊥AB,CD⊥AB,∠1与∠2互补.求证:DE⊥AC.
已知,如图,AC⊥BC,HF⊥AB,CD⊥AB,∠1与∠2互补.求证:DE⊥AC.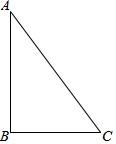 实践操作:如图,在Rt△ABC中,∠ABC=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法):
实践操作:如图,在Rt△ABC中,∠ABC=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法):