题目内容
1. 如图,⊙O经过点A,B,C,∠B=60°,AC=3cm,求⊙O的直径.
如图,⊙O经过点A,B,C,∠B=60°,AC=3cm,求⊙O的直径.
分析 首先根据题意作出图形,然后作直径AD,连接CD,由直径所对的圆周角是直角,可得∠ACD=90°,又由圆周角定理可得∠D=∠B=60°,然后由三角函数的知识求得答案.
解答  解:如图,作直径AD,连接CD,
解:如图,作直径AD,连接CD,
∴∠ACD=90°,
∵∠D=∠B=60°,AC=3cm,
∴AD=$\frac{AC}{sin∠D}$=$\frac{3}{\frac{\sqrt{3}}{2}}$=2$\sqrt{3}$cm.
点评 此题考查了三角形的外接圆的性质、圆周角定理以及三角函数等知识.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,M是线段AC中点,B在线段AC上,且AB=2cm、BC=2AB,求BM长度.
如图,M是线段AC中点,B在线段AC上,且AB=2cm、BC=2AB,求BM长度.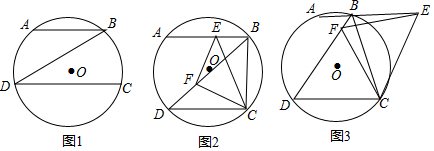
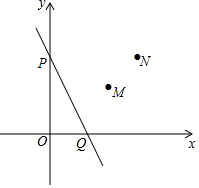 如图,直线l:y=-2x+b与两轴交于点P和点Q,点M(3,2),N(4,4)是第一象限内的两点
如图,直线l:y=-2x+b与两轴交于点P和点Q,点M(3,2),N(4,4)是第一象限内的两点