题目内容
15.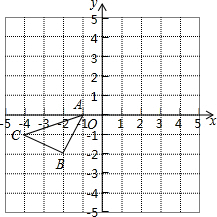 如图,所示的正方形网格中,△ABC的顶点均在格点上,在所给平面直角坐标系中解答下列问题:
如图,所示的正方形网格中,△ABC的顶点均在格点上,在所给平面直角坐标系中解答下列问题:(1)画出△ABC关于x轴对称的△A1B1C1;
(2)作出将△ABC绕原点O按逆时针方向旋转90°后所得的△A2B2C2;
(3)写出点A1、A2的坐标.
分析 (1)利用关于x轴对称的点的坐标特征写出点A、B、C的对应点A1、B1、C1的坐标,然后描点即可;
(2)利用网格特点和旋转的性质画出点A、B、C的对应点A2、B2、C2,从而得到△A2B2C2;
(3)由所画图形易得点A1、A2的坐标.
解答 解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作;
(3)点A1、A2的坐标分别为((-1,0),((0,-1).
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了轴对称变换.

练习册系列答案
相关题目
5.下列式子正确的是( )
| A. | -52=(-5)×(-5) | B. | 32=3×2 | C. | 32=3+3 | D. | -(-$\frac{1}{2}$)2=-$\frac{1}{2}$×$\frac{1}{2}$ |
7. 如图,直线AB∥CD,BC平分∠ABD,若∠1=65°,则∠2的大小为( )
如图,直线AB∥CD,BC平分∠ABD,若∠1=65°,则∠2的大小为( )
 如图,直线AB∥CD,BC平分∠ABD,若∠1=65°,则∠2的大小为( )
如图,直线AB∥CD,BC平分∠ABD,若∠1=65°,则∠2的大小为( )| A. | 35° | B. | 40° | C. | 50° | D. | 65° |
5.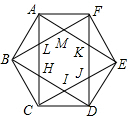 如图,正六边形ABCDEF的边长为6,连接对角线AC,BD,CE,DF,EA,FB,这些对角线相交得到正六边形HUKML,则得到的正六边形HUKML的面积为( )
如图,正六边形ABCDEF的边长为6,连接对角线AC,BD,CE,DF,EA,FB,这些对角线相交得到正六边形HUKML,则得到的正六边形HUKML的面积为( )
 如图,正六边形ABCDEF的边长为6,连接对角线AC,BD,CE,DF,EA,FB,这些对角线相交得到正六边形HUKML,则得到的正六边形HUKML的面积为( )
如图,正六边形ABCDEF的边长为6,连接对角线AC,BD,CE,DF,EA,FB,这些对角线相交得到正六边形HUKML,则得到的正六边形HUKML的面积为( )| A. | 18$\sqrt{3}$ | B. | 36$\sqrt{3}$ | C. | $\frac{9\sqrt{3}}{2}$ | D. | $\frac{18\sqrt{3}}{2}$ |
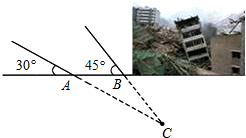 一方有难八方支援.安徽地震局救援队在某次地震救援中,探测出某建筑物废墟下方点C处有生命迹象,在废墟一侧某面上选两探测点A、B,AB相距2.1米,探测线与地面的夹角分别是35°和45°(如图),试确定生命所在点C与探测面的距离(参考数据$\sqrt{2}$≈1.4,≈1.7)
一方有难八方支援.安徽地震局救援队在某次地震救援中,探测出某建筑物废墟下方点C处有生命迹象,在废墟一侧某面上选两探测点A、B,AB相距2.1米,探测线与地面的夹角分别是35°和45°(如图),试确定生命所在点C与探测面的距离(参考数据$\sqrt{2}$≈1.4,≈1.7) 如图,边长为8cm的正方形ABCD先向上平移4cm,再向右平移2cm,得到正方形A′B′C′D′,此时阴影部分的面积为24cm2.
如图,边长为8cm的正方形ABCD先向上平移4cm,再向右平移2cm,得到正方形A′B′C′D′,此时阴影部分的面积为24cm2. 如图,在△ABC中,AD是高,AE是角平分线,∠B=20°,∠C=60°.求∠CAD和∠AEC的度数.
如图,在△ABC中,AD是高,AE是角平分线,∠B=20°,∠C=60°.求∠CAD和∠AEC的度数.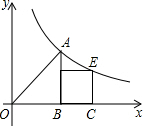 在平面直角坐标系中,等腰直角△OAB的直角边OB和正方形BCEF的一边BC都在x轴的正半轴上,函数y=$\frac{k}{x}$(k>0)的图象过点A,E.若BC=1,则k的值等于$\frac{3+\sqrt{5}}{2}$.
在平面直角坐标系中,等腰直角△OAB的直角边OB和正方形BCEF的一边BC都在x轴的正半轴上,函数y=$\frac{k}{x}$(k>0)的图象过点A,E.若BC=1,则k的值等于$\frac{3+\sqrt{5}}{2}$.