题目内容
6.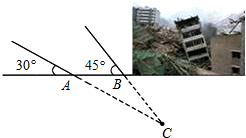 一方有难八方支援.安徽地震局救援队在某次地震救援中,探测出某建筑物废墟下方点C处有生命迹象,在废墟一侧某面上选两探测点A、B,AB相距2.1米,探测线与地面的夹角分别是35°和45°(如图),试确定生命所在点C与探测面的距离(参考数据$\sqrt{2}$≈1.4,≈1.7)
一方有难八方支援.安徽地震局救援队在某次地震救援中,探测出某建筑物废墟下方点C处有生命迹象,在废墟一侧某面上选两探测点A、B,AB相距2.1米,探测线与地面的夹角分别是35°和45°(如图),试确定生命所在点C与探测面的距离(参考数据$\sqrt{2}$≈1.4,≈1.7)
分析 首先过C作CD⊥AB,设CD=x米,则DB=CD=x米,AD=$\sqrt{3}$CD=$\sqrt{3}$x米,再根据AB相距2.1米可得方程$\sqrt{3}$x-x=2.1,再解即可.
解答 解:过C作CD⊥AB,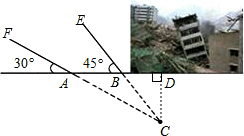
设CD=x米,
∵∠ABE=45°,
∴∠CBD=45°,
∴DB=CD=x米,
∵∠CAD=30°,
∴AD=$\sqrt{3}$CD=$\sqrt{3}$x米,
∵AB相距2.1米,
∴$\sqrt{3}$x-x=2.1,
解得:x=3.
答:命所在点C与探测面的距离是3米.
点评 此题主要考查了解直角三角形的应用,关键是正确分析出CD、AD、BD的关系.

练习册系列答案
相关题目
1.已知:a、b、c是三角形ABC的三边,化简:|a-b-c|+|a+b-c|结果是( )
| A. | 2a-2c | B. | 2b | C. | 2a | D. | 2b-2a |
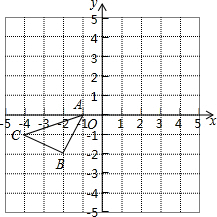 如图,所示的正方形网格中,△ABC的顶点均在格点上,在所给平面直角坐标系中解答下列问题:
如图,所示的正方形网格中,△ABC的顶点均在格点上,在所给平面直角坐标系中解答下列问题: