题目内容
14.下列命题正确的有( )①如果等腰三角形的底角为15°,那么腰上的高是腰长的一半;
②三角形至少有一个内角不大于60°;
③连结任意四边形各边中点形成的新四边形是平行四边形;
④十边形内角和为1800°.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 利用等腰三角形的性质、三角形的三边关系、中点四边形及多边形的内角和的知识进行判断后即可确定正确的选项.
解答 解:①如果等腰三角形的底角为15°,那么腰上的高是腰长的一半,正确,
证明如下:如图:
∵∠B=∠ACB=15°,
∴∠CAB=150°,
∴∠CAD=30°,CD⊥AB,
∴在直角三角形ACD中,CD=$\frac{1}{2}$AC;
②因为三角形的内角和等于180°,所以一个三角形中至少有一个内角不大于60°,所以三角形至少有一个内角不大于60°正确;
③连结任意四边形各边中点形成的新四边形是平行四边形,正确,
证明如下:】证明:如图,连接AC,
∵E、F、G、H分别是四边形ABCD边的中点,
∴HG∥AC,HG=$\frac{1}{2}$AC,EF∥AC,EF=$\frac{1}{2}$AC;
∴EF=HG且EF∥HG;
∴四边形EFGH是平行四边形.
故答案是:平行四边形.;
④十边形内角和为(10-2)×180=1440°,故错误,
正确有3个,
故选C.
点评 本题考查了命题与定理的知识,解题的关键是了解等腰三角形的性质、三角形的三边关系、中点四边形及多边形的内角和的知识,难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.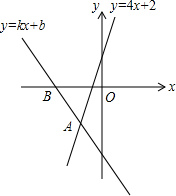 如图,经过点B(-2,0)的直线y=kx+b与直线y=kx+b相交于点A(-1,-2),则不等式4x+2<kx+b<0的解集为( )
如图,经过点B(-2,0)的直线y=kx+b与直线y=kx+b相交于点A(-1,-2),则不等式4x+2<kx+b<0的解集为( )
 如图,经过点B(-2,0)的直线y=kx+b与直线y=kx+b相交于点A(-1,-2),则不等式4x+2<kx+b<0的解集为( )
如图,经过点B(-2,0)的直线y=kx+b与直线y=kx+b相交于点A(-1,-2),则不等式4x+2<kx+b<0的解集为( )| A. | -2<x<-1 | B. | -2$<x<-\frac{1}{2}$ | C. | -1$<x<-\frac{1}{2}$ | D. | -$\frac{1}{2}<x<0$ |
15.若a>b,则下列各式不一定成立的是( )
| A. | $\frac{1}{a}<\frac{1}{b}$ | B. | $-\frac{a}{3}-2<-\frac{b}{3}-2$ | C. | a+1>b | D. | -2a<-2b |
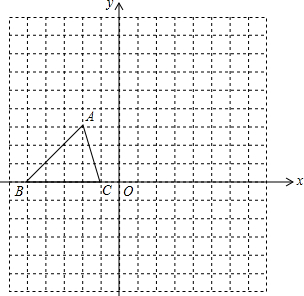 如图所示,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
如图所示,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0). 如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AB=1,则AC的长为2.
如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AB=1,则AC的长为2. 已知:如图所示,E为正方形ABCD外一点,AE=AD,∠ADE=75°,求∠AEB的度数.
已知:如图所示,E为正方形ABCD外一点,AE=AD,∠ADE=75°,求∠AEB的度数.