Question

4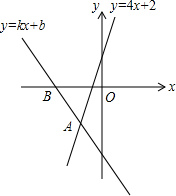．如图，经过点B（-2，0）的直线y=kx+b与直线y=kx+b相交于点A（-1，-2），则不等式4x+2＜kx+b＜0的解集为（　　）

• A． -2＜x＜-1
• B． -2$＜x＜-\frac{1}{2}$
• C． -1$＜x＜-\frac{1}{2}$
• D． -$\frac{1}{2}＜x＜0$

Answer 1

分析 由图象得到直线y=kx+b与直线y=4x+2的交点A的坐标（-1，-2）及直线y=kx+b与x轴的交点坐标，观察直线y=4x+2落在直线y=kx+b的下方且直线y=kx+b落在x轴下方的部分对应的x的取值即为所求．

解答 解：∵经过点B（-2，0）的直线y=kx+b与直线y=4x+2相交于点A（-1，-2），
∴直线y=kx+b与直线y=4x+2的交点A的坐标为（-1，-2），直线y=kx+b与x轴的交点坐标为B（-2，0），
又∵当x＜-1时，4x+2＜kx+b，
当x＞-2时，kx+b＜0，
∴不等式4x+2＜kx+b＜0的解集为-2＜x＜-1．
故选A．

点评 本题考查了一次函数与一元一次不等式的关系：从函数的角度看，就是寻求使一次函数y=ax+b的值大于（或小于）0的自变量x的取值范围；从函数图象的角度看，就是确定直线y=kx+b在x轴上（或下）方部分所有的点的横坐标所构成的集合．