题目内容
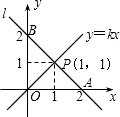 如图,在平面直角坐标系中,一条直线l:y=mx+b与x轴相交于点A(2,0),与y轴交于点B,与正比例函数y=kx(k≠0,为常数)的图象相交于点P(1,1)
如图,在平面直角坐标系中,一条直线l:y=mx+b与x轴相交于点A(2,0),与y轴交于点B,与正比例函数y=kx(k≠0,为常数)的图象相交于点P(1,1)(1)求k的值及直线l的解析式;
(2)求△POB的面积;
(3)在正比例函数y=kx上存在着点Q,使得△QOA的面积是△POB面积的2倍,直接写出Q点坐标.
考点:两条直线相交或平行问题
专题:
分析:(1)将P点坐标代入y=kx中求k的值即可,再将(1,1),(2,0)代入y=mx+b求出即可;
(2)已知B点纵坐标和P点横坐标,根据三角形面积公式,可求△BOP的面积;
(3)利用(2)中所求,进而得出Q点纵坐标,即可得出其横坐标.
(2)已知B点纵坐标和P点横坐标,根据三角形面积公式,可求△BOP的面积;
(3)利用(2)中所求,进而得出Q点纵坐标,即可得出其横坐标.
解答:解:(1)将点P(1,1)代入直线y=kx中,
得k=1;
将(2,0),(1,1)代入y=mx+b得:
,
解得:
,
∴直线l的解析式为:y=-x+2;
(2)如图,S△BOP=
×2×1=1;
(3)∵△QOA的面积是△POB面积的2倍,AO=2,S△QOA=2,
∴Q点的纵坐标为:2或-2,
当y=2,则x=2,
当y=-2,则x=-2,
∴Q点坐标为:(2,2),(-2,-2).
得k=1;
将(2,0),(1,1)代入y=mx+b得:
|
解得:
|
∴直线l的解析式为:y=-x+2;
(2)如图,S△BOP=
| 1 |
| 2 |
(3)∵△QOA的面积是△POB面积的2倍,AO=2,S△QOA=2,
∴Q点的纵坐标为:2或-2,
当y=2,则x=2,
当y=-2,则x=-2,
∴Q点坐标为:(2,2),(-2,-2).
点评:本题考查了一次函数的综合运用.关键是结合图形特点,根据三角形面积公式求面积,分类讨论,求Q点的坐标.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
 假如一个儿童走在如图的地板上,当他随意停下时(停在正方形内),他最终停在地板上阴影部分的概率是( )
假如一个儿童走在如图的地板上,当他随意停下时(停在正方形内),他最终停在地板上阴影部分的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
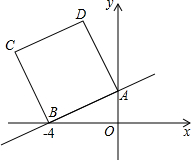 如图,已知直线y=
如图,已知直线y=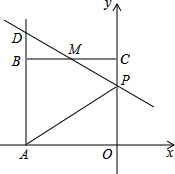 如图,已知正方形OABC的边长为2,顶点A、C分别在x轴的负半轴和y轴的正半轴上,M是BC的中点.P(0,m)是线段OC上一动点(C点除外),直线PM交AB的延长线于点D.
如图,已知正方形OABC的边长为2,顶点A、C分别在x轴的负半轴和y轴的正半轴上,M是BC的中点.P(0,m)是线段OC上一动点(C点除外),直线PM交AB的延长线于点D.