题目内容
假如一个儿童走在如图的地板上，当他随意停下时（停在正方形内），他最终停在地板上阴影部分的概率是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
考点：几何概率
专题：
分析：根据几何概率的求法：最终停留在黑色的方砖上的概率就是黑色区域的面积与总面积的比值．
解答：解：观察这个图可知：黑色区域（4块）的面积占总面积（16块）的
，故其概率为
．
故选：D．
| 1 |
| 4 |
| 1 |
| 4 |
故选：D．
点评：本题考查几何概率的求法：首先根据题意将代数关系用面积表示出来，一般用阴影区域表示所求事件（A）；然后计算阴影区域的面积在总面积中占的比例，这个比例即事件（A）发生的概率．
练习册系列答案
阅读快车系列答案
相关题目
如图几何体的左视图是（ ）A、 |
B、 |
C、 |
D、 |
从1，2，3，4，5中随机取出三个不同的数，则其和为奇数的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，点A（x1，y1），B（x2，y2）在抛物线y=| 1 |
| 4 |
①点（x1，x2）在反比例函数y=-
| 16 |
| x |
②直线AB与y轴交于定点（0，4）；
③若以AB为直径的圆与x轴相切，则y1+y2=8．
其中正确的结论是（ ）
| A、①② | B、①③ | C、②③ | D、①②③ |
已知下列命题：
（1）若|a|≠|b|，则a≠b；
（2）若a2＞b2，且a，b均为负数，则a＜b；
（3）若a＞b，且c=d＞0，则ac＞bd；
（4）若a＞b，则ac2＞bc2
其中原命题与逆命题均为真命题的是（ ）
（1）若|a|≠|b|，则a≠b；
（2）若a2＞b2，且a，b均为负数，则a＜b；
（3）若a＞b，且c=d＞0，则ac＞bd；
（4）若a＞b，则ac2＞bc2
其中原命题与逆命题均为真命题的是（ ）
| A、（1）（3） |
| B、（2）（3） |
| C、（1）（2） |
| D、（1）（4） |
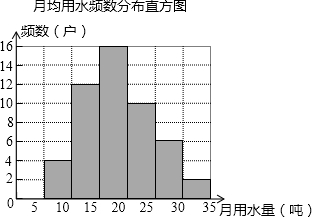每年的3月22日被联合国为世界水日，旨在唤起公众的水意识，加强水资源保护．为响应号召，小聪同学随机调查了某小区部分家庭月均用水量并将调查数据进行整理，绘制频数分布直方图如图，则被抽查的用户中月均用水落在20～25（吨）的频率是（ ）
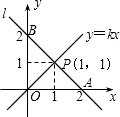如图，在平面直角坐标系中，一条直线l：y=mx+b与x轴相交于点A（2，0），与y轴交于点B，与正比例函数y=kx（k≠0，为常数）的图象相交于点P（1，1）