题目内容
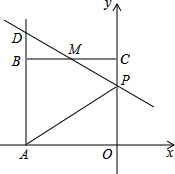 如图,已知正方形OABC的边长为2,顶点A、C分别在x轴的负半轴和y轴的正半轴上,M是BC的中点.P(0,m)是线段OC上一动点(C点除外),直线PM交AB的延长线于点D.
如图,已知正方形OABC的边长为2,顶点A、C分别在x轴的负半轴和y轴的正半轴上,M是BC的中点.P(0,m)是线段OC上一动点(C点除外),直线PM交AB的延长线于点D.(1)求点D的坐标(用含m的代数式表示);
(2)当△APD是以AP为腰的等腰三角形时,求m的值.
考点:待定系数法求一次函数解析式,等腰三角形的性质
专题:
分析:(1)证明Rt△PMC≌Rt△DMB,即可证明DB=2-m,AD=4-m,从而求解;
(2)分AP=AD,PD=PA,PD=DA三种情况,根据勾股定理即可求解.
(2)分AP=AD,PD=PA,PD=DA三种情况,根据勾股定理即可求解.
解答:解:(1)由题意得CM=BM,
∵∠PMC=∠DMB,
∴Rt△PMC≌Rt△DMB,
∴DB=PC,
∴DB=2-m,AD=4-m,
∴点D的坐标为(-2,4-m).
(2)分三种情况
①若AP=AD,则4+m2=(4-m)2,解得m=
;
②若PD=PA
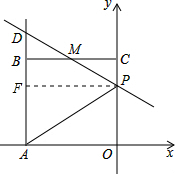
过P作PF⊥AB于点F(如图),
则AF=FD=
AD=
(4-m)
又∵OP=AF,
∴m=
(4-m)则m=
③若PD=DA,
∵△PMC≌△DMB,
∴PM=
PD=
AD=
(4-m),
∵PC2+CM2=PM2,
∴(2-m)2+1=
(4-m)2,
解得m1=
,m2=2(舍去).
综上所述,当△APD是等腰三角形时,m的值为
或
或
.
∵∠PMC=∠DMB,
∴Rt△PMC≌Rt△DMB,
∴DB=PC,
∴DB=2-m,AD=4-m,
∴点D的坐标为(-2,4-m).
(2)分三种情况
①若AP=AD,则4+m2=(4-m)2,解得m=
| 3 |
| 2 |
②若PD=PA
过P作PF⊥AB于点F(如图),
则AF=FD=
| 1 |
| 2 |
| 1 |
| 2 |
又∵OP=AF,
∴m=
| 1 |
| 2 |
| 4 |
| 3 |

③若PD=DA,
∵△PMC≌△DMB,
∴PM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵PC2+CM2=PM2,
∴(2-m)2+1=
| 1 |
| 4 |
解得m1=
| 2 |
| 3 |
综上所述,当△APD是等腰三角形时,m的值为
| 3 |
| 2 |
| 4 |
| 3 |
| 2 |
| 3 |
点评:此题考查等腰三角形的性质,三角形全等的判定与性质,以及分类讨论思想的渗透.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图几何体的左视图是( )
如图几何体的左视图是( )A、 |
B、 |
C、 |
D、 |
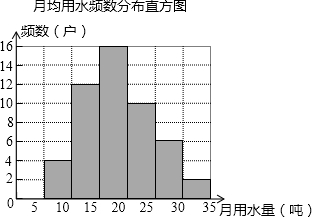 每年的3月22日被联合国为世界水日,旨在唤起公众的水意识,加强水资源保护.为响应号召,小聪同学随机调查了某小区部分家庭月均用水量并将调查数据进行整理,绘制频数分布直方图如图,则被抽查的用户中月均用水落在20~25(吨)的频率是( )
每年的3月22日被联合国为世界水日,旨在唤起公众的水意识,加强水资源保护.为响应号召,小聪同学随机调查了某小区部分家庭月均用水量并将调查数据进行整理,绘制频数分布直方图如图,则被抽查的用户中月均用水落在20~25(吨)的频率是( )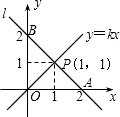 如图,在平面直角坐标系中,一条直线l:y=mx+b与x轴相交于点A(2,0),与y轴交于点B,与正比例函数y=kx(k≠0,为常数)的图象相交于点P(1,1)
如图,在平面直角坐标系中,一条直线l:y=mx+b与x轴相交于点A(2,0),与y轴交于点B,与正比例函数y=kx(k≠0,为常数)的图象相交于点P(1,1)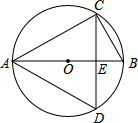 如图,在⊙O中,AB为⊙O的直径,C、D为⊙O上两点,弦AC=
如图,在⊙O中,AB为⊙O的直径,C、D为⊙O上两点,弦AC=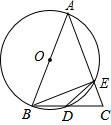 已知,如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°.
已知,如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°.