题目内容
有一列数，按一定规律排列为1，-4，16，-64，256，-1024…，其中有三个相邻的数的和是-13312，求着这三个数分别是多少？
考点：规律型：数字的变化类,一元一次方程的应用
专题：
分析：首先要观察这列数，发现：每相邻的三个数的比值是-4．若设其中一个，即可表示其它两个．
解答：解：设相邻三个数中的第一个数为x，那么第二个数为-4x，第三个数为16x．
由题意得x-4x+16x=-13312
解这个方程得x=-1024
所以-4x=4096
16x=-16384；
答：这三个数是-1024，4096，-16384．
由题意得x-4x+16x=-13312
解这个方程得x=-1024
所以-4x=4096
16x=-16384；
答：这三个数是-1024，4096，-16384．
点评：此题是一道找规律的题目，要求学生通过观察，分析、归纳发现其中的规律，并应用发现的规律解决问题．能够发现每相邻的三个数之间的规律，进一步列方程求解．
练习册系列答案
相关题目
已知下列命题：
（1）若|a|≠|b|，则a≠b；
（2）若a2＞b2，且a，b均为负数，则a＜b；
（3）若a＞b，且c=d＞0，则ac＞bd；
（4）若a＞b，则ac2＞bc2
其中原命题与逆命题均为真命题的是（ ）
（1）若|a|≠|b|，则a≠b；
（2）若a2＞b2，且a，b均为负数，则a＜b；
（3）若a＞b，且c=d＞0，则ac＞bd；
（4）若a＞b，则ac2＞bc2
其中原命题与逆命题均为真命题的是（ ）
| A、（1）（3） |
| B、（2）（3） |
| C、（1）（2） |
| D、（1）（4） |
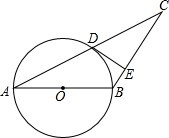已知：如图，AB是⊙O的直径，⊙O过AC的中点D，DE切⊙O于点D，交BC于点E．
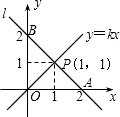如图，在平面直角坐标系中，一条直线l：y=mx+b与x轴相交于点A（2，0），与y轴交于点B，与正比例函数y=kx（k≠0，为常数）的图象相交于点P（1，1）