题目内容
19.某商场销售A、B两种品牌的教学设备,其进价分别为1.5万元/套,1.2万元/套;售价分别为1.65万元/套、1.4万元/套.该商场计划购进两种教学设备各若干套,共需66万元,全部销售后可获毛利润9万元.(1)设该商场计划购进A、B两种品牌的教学设备各x套、y套,求x,y的值.
(2)调研后,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少数量的1.5倍,采购进资金不超过69万元,问A种设备购进量至多减少多少套?
分析 (1)首先设该商场计划购进A,B两种品牌的教学设备分别为x套,y套,根据题意即可列方程组$\left\{\begin{array}{l}{1.5x+1.2y=66}\\{0.15x+0.2y=9}\end{array}\right.$,解此方程组即可求得答案;
(2)首先设A种设备购进数量减少a套,则B种设备购进数量增加1.5a套,根据题意即可列不等式1.5(20-a)+1.2(30+1.5a)≤69,解此不等式组即可求得答案.
解答 解:(1)设该商场计划购进A,B两种品牌的教学设备分别为x套,y套,
$\left\{\begin{array}{l}{1.5x+1.2y=66}\\{0.15x+0.2y=9}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=20}\\{y=30}\end{array}\right.$,
答:该商场计划购进A,B两种品牌的教学设备分别为20套,30套;
(2)设A种设备购进数量减少a套,则B种设备购进数量增加1.5a套,
1.5(20-a)+1.2(30+1.5a)≤69,
解得:a≤10,
答:A种设备购进数量至多减少10套.
点评 此题考查了一元一次不等式与二元一次方程组的应用.解决问题的关键是读懂题意,找到关键描述语,找到所求的量的等量关系和不等关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.“滴滴打车”深受大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按p元/千米计算,耗时费按q元/分钟计算.小明、小亮两人用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与车速如表:
(1)求p,q的值;
(2)“滴滴”推出新政策,在原有付费基础上,当里程数超过8千米后,超出的部分要加收0.6元/千米的里程费.某天,小丽两次使用“滴滴打车”共花费52元,总里程20千米,已知两次“滴滴打车”行驶的平均速度为40千米/小时,求小丽第一次“滴滴打车”的里程数?
| 时间(分钟) | 里程数(千米) | 车费(元) | |
| 小明 | 7 | 5 | 12.1 |
| 小亮 | 6 | 4.5 | 10.8 |
(2)“滴滴”推出新政策,在原有付费基础上,当里程数超过8千米后,超出的部分要加收0.6元/千米的里程费.某天,小丽两次使用“滴滴打车”共花费52元,总里程20千米,已知两次“滴滴打车”行驶的平均速度为40千米/小时,求小丽第一次“滴滴打车”的里程数?
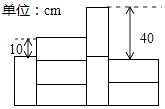 如图所示是由截面为同一种矩形的墙砖粘贴的部分墙面,其中三块横放的墙砖比一块竖放的墙砖高10cm,两块横放的墙砖比两块竖放的墙砖低40cm,则每块墙砖的截面面积是525cm2.
如图所示是由截面为同一种矩形的墙砖粘贴的部分墙面,其中三块横放的墙砖比一块竖放的墙砖高10cm,两块横放的墙砖比两块竖放的墙砖低40cm,则每块墙砖的截面面积是525cm2.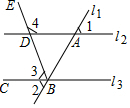 如图所示,直线l1与l2,l3相交于A,B两点,∠ABC的平分线交l2于点D,已知∠1=∠2=62°.
如图所示,直线l1与l2,l3相交于A,B两点,∠ABC的平分线交l2于点D,已知∠1=∠2=62°.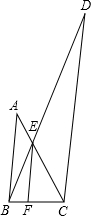 如图,AB∥EF∥CD,已知AB=20,BC=10,CD=80,求EF的值.
如图,AB∥EF∥CD,已知AB=20,BC=10,CD=80,求EF的值. 如图∠C=∠D=90°,要使△ABC≌△BAD需要添加的一个条件是∠CAB=∠DBA.
如图∠C=∠D=90°,要使△ABC≌△BAD需要添加的一个条件是∠CAB=∠DBA.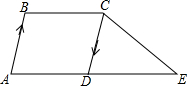 如图,在?ABCD中,点E在边AD的延长线上,DE=AD,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$.
如图,在?ABCD中,点E在边AD的延长线上,DE=AD,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$. 如图,AB是⊙O的直径,C为⊙O上一点,MN过C点,AD⊥MN于D,AC平分∠DAB.求证:MN为⊙O的切线.
如图,AB是⊙O的直径,C为⊙O上一点,MN过C点,AD⊥MN于D,AC平分∠DAB.求证:MN为⊙O的切线.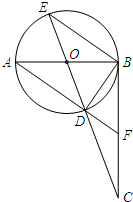 如图,AB是⊙O的直径,BC⊥AB,垂足为点B,连接CO并延长交⊙O于点D、E,连接AD并延长交BC于点F,则下列结论正确的有( )
如图,AB是⊙O的直径,BC⊥AB,垂足为点B,连接CO并延长交⊙O于点D、E,连接AD并延长交BC于点F,则下列结论正确的有( )