题目内容
已知有两张全等的矩形纸片．将两张纸片叠合成如图，请判断四边形ABCD的形状，并说明理由．考点：菱形的判定
专题：
分析：利用平行四边形的判定得出四边形ABCD是平行四边形，进而利用平行四边形面积求出BC=CD，进而得出答案．
解答：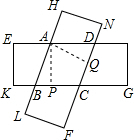
解：四边形ABCD是菱形．
理由：作AP⊥BC于P，AQ⊥CD于Q，
由题意知：AD∥BC，AB∥CD，
∴四边形ABCD是平行四边形，
∵两个矩形全等，
∴AP=AQ，
∵AP•BC=AQ•CD，
∴BC=CD，
∴平行四边形ABCD是菱形．
解：四边形ABCD是菱形．理由：作AP⊥BC于P，AQ⊥CD于Q，
由题意知：AD∥BC，AB∥CD，
∴四边形ABCD是平行四边形，
∵两个矩形全等，
∴AP=AQ，
∵AP•BC=AQ•CD，
∴BC=CD，
∴平行四边形ABCD是菱形．
点评：此题主要考查了菱形的判定以及平行四边形的判定，得出BC=CD是解题关键．
练习册系列答案
相关题目
如图，AB∥CD，EG⊥AB，∠1=50°，则∠E的度数等于（ ）| A、30° | B、40° |
| C、50° | D、60° |
已知等腰三角形的两条边长分别为2和4，则它的周长为（ ）
| A、8 | B、10 | C、6 | D、10或8 |
下列判断不正确的是（ ）
| A、若a＞b，则-4a＜-4b |
| B、若2a＞3a，则a＜0 |
| C、若a＞b，则ac2＞bc2 |
| D、若ac2＞bc2，则a＞b |
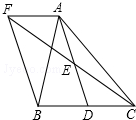如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，且AF=BD，连接BF．
某游乐场每天的赢利额y（元）与售出的门票x（张）之间的函数关系如图所示．