题目内容
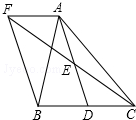 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.(1)证明:BD=CD;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
考点:全等三角形的判定与性质,矩形的判定
专题:计算题
分析:(1)由AF与BC平行,利用两直线平行内错角相等得到一对角相等,再一对对顶角相等,且由E为AD的中点,得到AE=DE,利用AAS得到三角形AFE与三角形DCE全等,利用全等三角形的对应边相等即可得证;
(2)当△ABC满足:AB=AC时,四边形AFBD是矩形,理由为:由AF与BD平行且相等,得到四边形AFBD为平行四边形,再由AB=AC,BD=CD,利用三线合一得到AD垂直于BC,即∠ADB为直角,即可得证.
(2)当△ABC满足:AB=AC时,四边形AFBD是矩形,理由为:由AF与BD平行且相等,得到四边形AFBD为平行四边形,再由AB=AC,BD=CD,利用三线合一得到AD垂直于BC,即∠ADB为直角,即可得证.
解答:解:(1)∵AF∥BC,
∴∠AFE=∠DCE,
∵E为AD的中点,
∴AE=DE,
在△AFE和△DCE中,
,
∴△AFE≌△DCE(AAS),
∴AF=CD,
∵AF=BD,
∴CD=BD;
(2)当△ABC满足:AB=AC时,四边形AFBD是矩形,
理由如下:∵AF∥BD,AF=BD,
∴四边形AFBD是平行四边形,
∵AB=AC,BD=CD,
∴∠ADB=90°,
∴四边形AFBD是矩形.
∴∠AFE=∠DCE,
∵E为AD的中点,
∴AE=DE,
在△AFE和△DCE中,
|
∴△AFE≌△DCE(AAS),
∴AF=CD,
∵AF=BD,
∴CD=BD;
(2)当△ABC满足:AB=AC时,四边形AFBD是矩形,
理由如下:∵AF∥BD,AF=BD,
∴四边形AFBD是平行四边形,
∵AB=AC,BD=CD,
∴∠ADB=90°,
∴四边形AFBD是矩形.
点评:此题考查了全等三角形的判定与性质,以及矩形的判定,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
下列运算正确的是( )
| A、m4•m2=m8 |
| B、(m2)3=m6 |
| C、(m-n)2=m2-n2 |
| D、3m-2m=2 |
电视机厂从2万台电视机中,抽取100台进行质量调查,在这个问题中表示正确的应该是( )
| A、20000台电视机是总体 |
| B、抽取的100台电视机是总体的一个样本 |
| C、2万台电视机的质量是总体 |
| D、每台电视机是个体 |
下列计算结果正确的是( )
| A、(a+3)(a-4)=a2-12 |
| B、(2x-3y)2=4x2-9y2 |
| C、(-3x2y)3=-9x6y3 |
| D、(x+2y)(2y-x)=4y2-x2 |
 已知有两张全等的矩形纸片.将两张纸片叠合成如图,请判断四边形ABCD的形状,并说明理由.
已知有两张全等的矩形纸片.将两张纸片叠合成如图,请判断四边形ABCD的形状,并说明理由.
 如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的路线移动(即:沿着长方形移动一周).
如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的路线移动(即:沿着长方形移动一周).