题目内容
14.有一块面积为(2a+b)2π的圆形木板,挖去一个圆后剩下的木板的面积是(2a-b)2π,问所挖去的圆的半径是多少?分析 可先求得挖去的圆的面积,再根据圆的面积公式可求得其半径.
解答 解:设所挖去的圆的面积为S,半径为r(r>0),
由题意可知
S=(2a+b)2π-(2a-b)2π
=π[(2a+b)2-(2a-b)2]
=π(2a+b+2a-b)(2a+b-2a+b)
=8abπ,
又∵S=πr2,
∴πr2=8abπ,
∴r2=8ab,
∴r=2$\sqrt{2ab}$,
即所挖去的圆的半径为2$\sqrt{2ab}$.
点评 本题主要考查因式分解的应用,利用因式分解计算出所挖去圆的面积是解题的关键.

练习册系列答案
相关题目
9.若|a|=8,|b|=6,且|a+b|=a+b,那么a-b的值只能是( )
| A. | 2 | B. | 14 | C. | 6 | D. | 2或14 |
3.有一个数阵排列如图:则第20行从左至右第10个数为( )


| A. | 425 | B. | 426 | C. | 427 | D. | 428 |
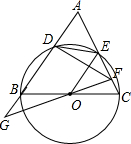 如图,在△ABC中,以BC为直径的⊙O,交AB、AC于点D、E,连接DE.
如图,在△ABC中,以BC为直径的⊙O,交AB、AC于点D、E,连接DE.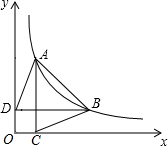 如图,已知双曲线y=$\frac{k}{x}$(x>0)图象上两点,过A、B两点分别作x轴、y轴的垂线,垂足分别为C、D,连接AD、BC,则:
如图,已知双曲线y=$\frac{k}{x}$(x>0)图象上两点,过A、B两点分别作x轴、y轴的垂线,垂足分别为C、D,连接AD、BC,则: