题目内容
9.若|a|=8,|b|=6,且|a+b|=a+b,那么a-b的值只能是( )| A. | 2 | B. | 14 | C. | 6 | D. | 2或14 |
分析 根据|a|=8,|b|=6,且|a+b|=a+b,即可确定a,b的值,从而求解.
解答 解:∵|a|=8,|b|=6,
∴a=±,8,b=±6,
又∵|a+b|=a+b,则a+b≥0
∴a=8,b=6或a=8,b=-6,
当a=6,b=6时,a-b=8-6=2;
当a=8,b=-6时,a-b=8+6=14.
故选D.
点评 本题主要考查了绝对值的性质,若x≠0,且|x|=a,则x=±a,根据任何数的绝对值一定是非负数,正确确定a,b的值,是解决本题的关键.

练习册系列答案
相关题目
1.下列说法不正确的是( )
| A. | -2.14既是负数、分数,也是有理数 | |
| B. | 0既不是正数也不是负数,但是整数 | |
| C. | 0是非正数 | |
| D. | -2012既是负数,也是整数,但不是有理数 |
1.已知3m2-2m-5=0,5n2+2n-3=0,其中m,n为实数,则|m-$\frac{1}{n}$|=( )
| A. | 0 | B. | $\frac{8}{3}$ | C. | $\frac{5}{3}$ | D. | 0或$\frac{8}{3}$ |
18.某中学举行书法比赛,各年龄组的参赛人数如下表所示:
则全体参赛选手年龄的平均数和中位数分别为( )
| 年龄组 | 13岁 | 14岁 | 15岁 | 16岁 |
| 参赛人数 | 9 | 15 | 3 | 3 |
| A. | 14.5,14.5 | B. | 14,15 | C. | 14.5,14 | D. | 14,14 |
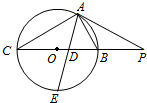 如图所示,PA为圆O的切线,A为切点,PBC是过点O的割线,PA=10,PB=5,∠CAB的平分线与BC和圆O分别交于点D和E.
如图所示,PA为圆O的切线,A为切点,PBC是过点O的割线,PA=10,PB=5,∠CAB的平分线与BC和圆O分别交于点D和E.