题目内容
8．计算：（1）（x2）3•（-x）2+x5•x3；
（2）（2x-1）（3x+2）；
（3）（5-x）（x+5）+（x+5）2；
（4）（-3）2-（π-3.14）0×2-2．
分析 （1）运用整式的混合运算顺序，按照先乘方后乘除，最后相加顺序运算，
（2）利用多项式乘多项式的方法求解即可，
（3）运用完全平方公式及平方差公式求解即可，
（4）利用零指数幂及负整数指数幂求解即可．
解答 解：（1）（x2）3•（-x）2+x5•x3；
=x6x2+x8，
=x8+x8，
=2x8，
（2）（2x-1）（3x+2）
=6x2+4x-3x-2，
=6x2+x-2；
（3）（5-x）（x+5）+（x+5）2；
=25-x2+x2+10x+25，
=10x+50；
（4）（-3）2-（π-3.14）0×2-2
=9-1×$\frac{1}{4}$，
=8$\frac{3}{4}$．
点评 本题主要考查了整式的混合运算，零指数幂及负整数指数幂，解题的关键是熟记整式的混合运算顺序，零指数幂及负整数指数幂法则．
练习册系列答案
名校课堂系列答案
相关题目
18．下列说法中正确的是（ ）
| A． | 36的平方根是6 | B． | 8的立方根是2 | ||
| C． | $\sqrt{4}$的平方根是±2 | D． | 9的算术平方根是-3 |
19．
如图，在平面直角坐标系xOy中，Rt△OA1C1，Rt△OA2C2，Rt△OA3C3，Rt△OA4C4…的斜边都在坐标轴上，∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4…=30°．若点A1的坐标为（3，0），OA1=OC2，OA2=OC3，OA3=OC4…，则依次规律，点A2016的纵坐标为（ ）
如图，在平面直角坐标系xOy中，Rt△OA1C1，Rt△OA2C2，Rt△OA3C3，Rt△OA4C4…的斜边都在坐标轴上，∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4…=30°．若点A1的坐标为（3，0），OA1=OC2，OA2=OC3，OA3=OC4…，则依次规律，点A2016的纵坐标为（ ）| A． | 0 | B． | -3×（$\frac{2}{3}$$\sqrt{3}$）2015 | C． | （2$\sqrt{3}$）2016 | D． | 3×（$\frac{2}{3}$$\sqrt{3}$）2015 |
13．
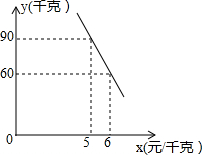某蔬菜经销商去蔬菜生产基地批发某种蔬菜，已知这种蔬菜的批发量在20千克～60千克之间（含20千克和60千克）时，每千克批发价是5元；若超过60千克时，批发的这种蔬菜全部打八折，但批发总金额不得少于300元．
（1）根据题意，填写如表：
（2）经调查，该蔬菜经销商销售该种蔬菜的日销售量y（千克）与零售价x（元/千克）是一次函数关系，其图象如图，求出y与x之间的函数关系式；
（3）若该蔬菜经销商每日销售此种蔬菜不低于75千克，且当日零售价不变，那么零售价定为多少时，该经销商销售此种蔬菜的当日利润最大？最大利润为多少元？
某蔬菜经销商去蔬菜生产基地批发某种蔬菜，已知这种蔬菜的批发量在20千克～60千克之间（含20千克和60千克）时，每千克批发价是5元；若超过60千克时，批发的这种蔬菜全部打八折，但批发总金额不得少于300元．（1）根据题意，填写如表：
| 蔬菜的批发量（千克） | … | 25 | 60 | 75 | 90 | … |
| 所付的金额（元） | … | 125 | 300 | 300 | 360 | … |
（3）若该蔬菜经销商每日销售此种蔬菜不低于75千克，且当日零售价不变，那么零售价定为多少时，该经销商销售此种蔬菜的当日利润最大？最大利润为多少元？
20．下列几何体中主视图、左视图、俯视图都相同的是（ ）
| A． |  | B． |  | C． |  | D． |  |