题目内容
4.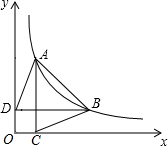 如图,已知双曲线y=$\frac{k}{x}$(x>0)图象上两点,过A、B两点分别作x轴、y轴的垂线,垂足分别为C、D,连接AD、BC,则:
如图,已知双曲线y=$\frac{k}{x}$(x>0)图象上两点,过A、B两点分别作x轴、y轴的垂线,垂足分别为C、D,连接AD、BC,则:(1)若A、B两点的坐标分别是(1,4)、(4,1),求S△OAB;
(2)证明:S△ABD=S△ABC.
(3)连接CD,判断CD与AB的位置关系,并说明理由.
分析 (1)作BH⊥x轴于H,如图,利用图形得到S△OAB+S△OBH=S△AOC+S梯形ACHB,根据反比例函数k的几何意义得S△OBH=S△AOC,所以S△OAB=S梯形ACHB,然后根据梯形得面积公式求解;
(2)根据反比例函数图象上点的坐标特征,设A(a,$\frac{k}{a}$),B(b,$\frac{k}{b}$),然后根据三角形面积公式可得S△ABD=S△ABC=$\frac{b-a}{2a}$k;
(3)由于S△ABD=S△ABC,根据三角形面积公式得到点C点和点D到AB的距离相等,所以CD∥AB.
解答  (1)解:作BH⊥x轴于H,如图,
(1)解:作BH⊥x轴于H,如图,
∵S△OAB+S△OBH=S△AOC+S梯形ACHB,
而S△OBH=S△AOC,
∴S△OAB=S梯形ACHB=$\frac{1}{2}$×(1+4)×(4-1)=$\frac{15}{2}$;
(2)证明:设A(a,$\frac{k}{a}$),B(b,$\frac{k}{b}$),
∵S△ABD=$\frac{1}{2}$•b•($\frac{k}{a}$-$\frac{k}{b}$)=$\frac{b-a}{2a}$k,
S△ABC=$\frac{1}{2}$•$\frac{k}{a}$•(b-a)=$\frac{b-a}{2a}$k,
∴S△ABD=S△ABC;
(3)解:CD∥AB.理由如下:
∵S△ABD=S△ABC,
∴CD∥AB.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了反比例函数k的几何意义和三角形面积公式.

练习册系列答案
相关题目
13.设对任意实数x,用[x]表示不大于x的最大整数,则对任意实数x,y,有( )
| A. | -[-x]=[x] | B. | [2x]=2[x] | C. | [x+y]≤[x]+[y] | D. | [x-y]≤[x]-[y] |
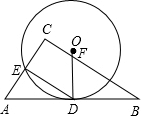 如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC交于点E,且DE∥BC,连接OD,与BC相交于点F
如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC交于点E,且DE∥BC,连接OD,与BC相交于点F