题目内容
19．古希腊数学家把数1，3，6，10，15，21，…叫做三角形数，它有一定的规律．若把第一个数记为a1，第二数记为a2，…，第n个数记为an．计算a2-a1，a3-a2，a4-a3，…，由此推算a10-a9=10，a2012=2025078．分析 先计算a2-a1=3-1=2；a3-a2=6-3=3；a4-a3=10-6=4，则a10-a9=10，a2=1+2，a3=1+2+3，a4=1+3+4，即第n个三角形数等于1到n的所有整数的和，然后计算n=2012的a的值．
解答 解：∵a2-a1=3-1=2；
a3-a2=6-3=3；
a4-a3=10-6=4，
∴a10-a9=10
∵a2=1+2，
a3=1+2+3，
a4=1+2+3+4，
…
∴a2012=1+2+3+4+…+2012=$\frac{2012×（2012+1）}{2}$=2025078．
故答案为：10，2025078．
点评 本题考查了规律型：数字的变化类，通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素，然后推广到一般情况是解答此题的关键．
练习册系列答案
相关题目
13．
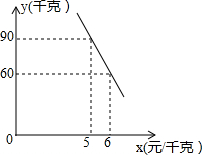某蔬菜经销商去蔬菜生产基地批发某种蔬菜，已知这种蔬菜的批发量在20千克～60千克之间（含20千克和60千克）时，每千克批发价是5元；若超过60千克时，批发的这种蔬菜全部打八折，但批发总金额不得少于300元．
（1）根据题意，填写如表：
（2）经调查，该蔬菜经销商销售该种蔬菜的日销售量y（千克）与零售价x（元/千克）是一次函数关系，其图象如图，求出y与x之间的函数关系式；
（3）若该蔬菜经销商每日销售此种蔬菜不低于75千克，且当日零售价不变，那么零售价定为多少时，该经销商销售此种蔬菜的当日利润最大？最大利润为多少元？
某蔬菜经销商去蔬菜生产基地批发某种蔬菜，已知这种蔬菜的批发量在20千克～60千克之间（含20千克和60千克）时，每千克批发价是5元；若超过60千克时，批发的这种蔬菜全部打八折，但批发总金额不得少于300元．（1）根据题意，填写如表：
| 蔬菜的批发量（千克） | … | 25 | 60 | 75 | 90 | … |
| 所付的金额（元） | … | 125 | 300 | 300 | 360 | … |
（3）若该蔬菜经销商每日销售此种蔬菜不低于75千克，且当日零售价不变，那么零售价定为多少时，该经销商销售此种蔬菜的当日利润最大？最大利润为多少元？
4．设P是高为h的正三角形内的一点，P到三边的距离分别为x，y，z（x≤y≤z）．若以x，y，z为边可以组成三角形，则z应满足的条件为（ ）
| A． | $\frac{1}{4}$h≤z$＜\frac{1}{3}$h | B． | $\frac{1}{3}$h≤z$＜\frac{1}{2}$h | C． | $\frac{1}{2}$h≤z$＜\frac{3}{4}$h | D． | $\frac{3}{4}h≤z＜h$ |