题目内容
6.若有奖储蓄每1000张奖券中,有一等奖1张,奖金500元,二等奖10张,奖金100元,三等奖50张,奖金20元,纪念奖100张,奖金5元.某人买一张奖券,则他得奖不少于20元的概率为$\frac{61}{1000}$.分析 首先根据题意,当这个人至少得到三等奖时,他得奖不少于20元;然后根据概率公式,用一、二、三等奖的数量和除以奖券的总量,求出他得奖不少于20元的概率为多少即可.
解答 解:(1+10+50)÷1000
=61÷1000
=$\frac{61}{1000}$
∴他得奖不少于20元的概率为$\frac{61}{1000}$.
故答案为:$\frac{61}{1000}$.
点评 此题主要考查了概率公式的应用,要熟练掌握,解答此题的关键是要明确:随机事件A的概率P(A)=事件A可能出现的结果数÷所有可能出现的结果数.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
20.下列几何体中主视图、左视图、俯视图都相同的是( )
| A. |  | B. |  | C. |  | D. |  |
1.下列说法不正确的是( )
| A. | -2.14既是负数、分数,也是有理数 | |
| B. | 0既不是正数也不是负数,但是整数 | |
| C. | 0是非正数 | |
| D. | -2012既是负数,也是整数,但不是有理数 |
1.已知3m2-2m-5=0,5n2+2n-3=0,其中m,n为实数,则|m-$\frac{1}{n}$|=( )
| A. | 0 | B. | $\frac{8}{3}$ | C. | $\frac{5}{3}$ | D. | 0或$\frac{8}{3}$ |
18.某中学举行书法比赛,各年龄组的参赛人数如下表所示:
则全体参赛选手年龄的平均数和中位数分别为( )
| 年龄组 | 13岁 | 14岁 | 15岁 | 16岁 |
| 参赛人数 | 9 | 15 | 3 | 3 |
| A. | 14.5,14.5 | B. | 14,15 | C. | 14.5,14 | D. | 14,14 |
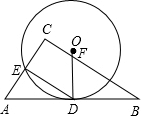 如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC交于点E,且DE∥BC,连接OD,与BC相交于点F
如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC交于点E,且DE∥BC,连接OD,与BC相交于点F