题目内容
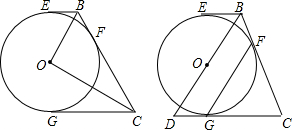
3.已知四边形ABCD是正方形,等腰直角△AEF的直角顶点E在直线上(不与点B重合),FM⊥AD,交边AD于点M,交BC于点H.(1)如图1,当E在CB的延长线上时,求证:AB=EB+AM;
(2)如图2,当E在BC的延长线上时,若BE=$\sqrt{3}$,△AFM=15°,求AM的长.

分析 (1)由等腰直角三角形的性质和正方形的性质得AE=EF,∠ABE=∠EHF=90°,由AAS证明△ABE≌△EHF,再利用全等三角形的性质定理可得结论;
(2)同(1)先证明△ABE≌△EHF,再利用全等三角形的性质定理可得BE=BH+EH=AM+AB;求出∠EFH=30°,由△ABE≌△EHF,根据全等三角形的性质易得∠AEB,利用锐角三角函数易得AB,即可得出AM的长.
解答 (1)证明:∵∠AEB+∠FEH=90°,∠AEB+∠EAB=90°,
∴∠FEH=∠EAB,
在△ABE与△EHF中,
$\left\{\begin{array}{l}{∠ABE=∠EHF}&{\;}\\{∠EAB=∠FEH}&{\;}\\{AE=FE}&{\;}\end{array}\right.$,
∴△ABE≌△EHF(AAS),
∴AB=EH=EB+BH=EB+AM;
(2)解:∠BAE+∠AEB=90°,∠AEB+∠HEF=90°,
∴∠BAE=∠HEF,
在△ABE与△EHF中,
$\left\{\begin{array}{l}{∠ABE=∠EHF}&{\;}\\{∠EAB=∠FEH}&{\;}\\{AE=FE}&{\;}\end{array}\right.$,
∴△ABE≌△EHF(AAS),
∴AB=EH,
∴BE=BH+EH=AM+AB;
∵∠AFM=15°,∠AFE=45°,
∴∠EFH=45°-15°=30°,
∴∠AEB=30°,
∵BE=$\sqrt{3}$,
∴AB=BE•tan30°=$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=1,
∵BE=AM+AB,
∴AM=BE-AB=$\sqrt{3}$-1.
点评 本题主要考查了等腰直角三角形的性质,正方形的性质,全等三角形的性质及判定定理;熟练掌握正方形的性质,证明三角形全等是解决问题的关键.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案| A. | 直角三角形 | B. | 等腰三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |
 “赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 50≤x<60 | 6 |
| 第2组 | 60≤x<70 | 8 |
| 第3组 | 70≤x<80 | 14 |
| 第4组 | 80≤x<90 | a |
| 第5组 | 90≤x<100 | 10 |
(1)①求表中a的值;②频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
| A. |  | B. |  | C. |  | D. |  |
| A. | a≥8 | B. | a<10 | C. | 8≤a≤10 | D. | 8≤a<10 |