题目内容
13.△ABC的三边满足|a+b-16|+$\sqrt{a-b-4}$+(c-8)2=0,则△ABC为( )| A. | 直角三角形 | B. | 等腰三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |
分析 首先利用绝对值以及偶次方的性质和二次根式的性质得出a,b,c的值,进而利用勾股定理的逆定理求出答案.
解答 解:∵|a+b-16|+$\sqrt{a-b-4}$+(c-8)2=0,
∴$\left\{\begin{array}{l}{a+b-16=0}\\{a-b-4=0}\\{c-8=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=10}\\{b=6}\\{c=8}\end{array}\right.$,
∵a2=b2+c2,
∴△ABC为直角三角形.
故选:A.
点评 此题主要考查了绝对值以及偶次方的性质和二次根式的性质和勾股定理的逆定理,正确得出a,b,c的值是解题关键.

练习册系列答案
相关题目
6.方程组$\left\{\begin{array}{l}{x-z=4}\\{z-2y=-1}\\{x+y-z=-1}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=7}\\{y=-5}\\{z=-11}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-7}\\{y=5}\\{z=-11}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-7}\\{y=-5}\\{z=-11}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=7}\\{y=-5}\\{z=11}\end{array}\right.$ |
5.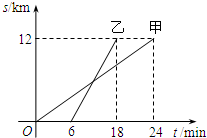 如图,表示甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.甲、乙两人前往目的地所行驶的路程s(km)随时间t(min)变化的函数图象,则每分钟乙比甲多行驶的路程为( )
如图,表示甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.甲、乙两人前往目的地所行驶的路程s(km)随时间t(min)变化的函数图象,则每分钟乙比甲多行驶的路程为( )
 如图,表示甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.甲、乙两人前往目的地所行驶的路程s(km)随时间t(min)变化的函数图象,则每分钟乙比甲多行驶的路程为( )
如图,表示甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.甲、乙两人前往目的地所行驶的路程s(km)随时间t(min)变化的函数图象,则每分钟乙比甲多行驶的路程为( )| A. | 1.5千米 | B. | 2千米 | C. | 0.5千米 | D. | 1千米 |
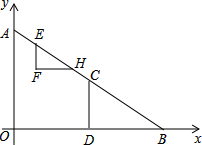 已知:在直角坐标系中,点A(0,6),B(8,0),点C是线段AB的中点,CD⊥OB交OB于点D,Rt△EFH的斜边EH在射线AB上,顶点F在射线AB的左侧,EF∥OA.点E从点A出发,以每秒1个单位的速度向点B运动,到点B停止.AE=EF,运动时间为t(秒).
已知:在直角坐标系中,点A(0,6),B(8,0),点C是线段AB的中点,CD⊥OB交OB于点D,Rt△EFH的斜边EH在射线AB上,顶点F在射线AB的左侧,EF∥OA.点E从点A出发,以每秒1个单位的速度向点B运动,到点B停止.AE=EF,运动时间为t(秒). 甲骑自行车从A地出发前往B地,同时乙步行从B地出发前往A地,如图所示,y甲、y乙分别表示甲、乙离开A地y(km)与已用时间x(h)之间的关系,且直线y甲与直线y乙相交于点M.
甲骑自行车从A地出发前往B地,同时乙步行从B地出发前往A地,如图所示,y甲、y乙分别表示甲、乙离开A地y(km)与已用时间x(h)之间的关系,且直线y甲与直线y乙相交于点M.