题目内容
20.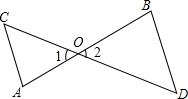 如图,AB和CD相交于点O,∠C=∠1,∠D=∠2,求证:∠A=∠B.
如图,AB和CD相交于点O,∠C=∠1,∠D=∠2,求证:∠A=∠B.证明:∵∠C=∠1,∠D=∠2(已知)
又∵∠1=∠2(对顶角相等)
∴∠C=∠D(等量代换)
∴AC∥BD(内错角相等,两直线平行)
∴∠A=∠B(两直线平行,内错角相等)
分析 根据对顶角相等可得∠1=∠2,再由∠C=∠1,∠D=∠2,等量代换可得∠C=∠D,然后根据内错角相等,两直线平行可判断出AC∥DB,最后根据两直线平行,内错角相等得出∠A=∠B.
解答 证明:∵∠C=∠1,∠D=∠2 (已知)
又∵∠1=∠2 ( 对顶角相等)
∴∠C=∠D( 等量代换)
∴AC∥BD ( 内错角相等,两直线平行)
∴∠A=∠B(两直线平行,内错角相等)
故答案为对顶角相等;∠C=∠D;内错角相等,两直线平行;∠A=∠B.
点评 本题考查了平行线的判定与性质,对顶角的性质,熟练掌握平行线的判定方法和性质,并准确识图是解题的关键.

练习册系列答案
相关题目
10.已知三角形的周长小于13,各边长均为整数且三边各不相等,那么这样的三角形个数共有( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
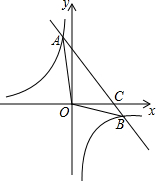 如图,已知一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象相交于点A(-2,m)和点B(4,-2),与x轴交于点C
如图,已知一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象相交于点A(-2,m)和点B(4,-2),与x轴交于点C