题目内容
17.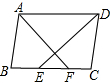 如图,在四边形ABCD中,AB=CD,∠ADC与∠BAD的平分线分别交BC于点E、F,且AF⊥DE,垂足为G
如图,在四边形ABCD中,AB=CD,∠ADC与∠BAD的平分线分别交BC于点E、F,且AF⊥DE,垂足为G(1)求证:四边形ABCD是平行四边形;
(2)若AB=4,AD=6,求CF的长.
分析 (1)由垂线的定义得出∠DAF+∠ADE=90°,由角平分线得出∠BAD+∠ADC=180°,证出AB∥CD,由AB=CD,即可证出四边形ABCD是平行四边形;
(2)由平行线的性质和角平分线证出∠BAF=∠AFB,得出BF=AB=4;同理:CE=CD=4,求出EF的长,即可得出CF的长.
解答 (1)证明:∵AF⊥DE,
∴∠DAF+∠ADE=90°,
∵∠ADC与∠BAD的平分线分别交BC于点E、F,
∴∠ADE=$\frac{1}{2}$∠ADC,∠DAF=$\frac{1}{2}$∠BAD,
∴∠BAD+∠ADC=180°,
∴AB∥CD,
∵AB=CD,
∴四边形ABCD是平行四边形;
(2)解:∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴CD=AB=4,BC=AD=6,AD∥CB,
∴∠DAF=∠AFB,
∴∠BAF=∠AFB,
∴BF=AB=4;
同理:CE=CD=4.
∴EF=BF+CE-BC═4+4-6=2,
∴CF=CE-EF=2.
点评 本题考查了平行四边形的判定与性质、平行线的判定、等腰三角形的判定;熟练掌握平行四边形的判定与性质是解决问题的关键.

练习册系列答案
相关题目
 如图,菱形ABCD的边长为4cm,且∠ABC=120°,E是BC的中点,在BD上求点P,使PC+PE取最小值,并求这个最小值.
如图,菱形ABCD的边长为4cm,且∠ABC=120°,E是BC的中点,在BD上求点P,使PC+PE取最小值,并求这个最小值.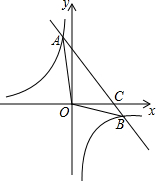 如图,已知一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象相交于点A(-2,m)和点B(4,-2),与x轴交于点C
如图,已知一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象相交于点A(-2,m)和点B(4,-2),与x轴交于点C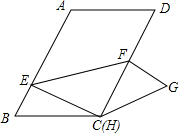 如图,在?ABCD中,AB=8,BC=6,∠B=60°,点E是边AB上的一点,点F是边CD上一点,将?ABCD沿EF折叠,得到四边形EFGH,点A的对应点为点H,点D的对应点为点G.
如图,在?ABCD中,AB=8,BC=6,∠B=60°,点E是边AB上的一点,点F是边CD上一点,将?ABCD沿EF折叠,得到四边形EFGH,点A的对应点为点H,点D的对应点为点G.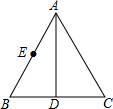 如图,已知AD是等边△ABC的角平分线,点E是AB的中点,且AD=6,BD=2$\sqrt{3}$,点M是AD上一动点,求△BEM的周长的最小值.
如图,已知AD是等边△ABC的角平分线,点E是AB的中点,且AD=6,BD=2$\sqrt{3}$,点M是AD上一动点,求△BEM的周长的最小值.