题目内容
13.若最简二次根式$\sqrt{{b}^{2}+2b+2}$与$\sqrt{3+2b}$是同类根式,则b的值是1.分析 依据同类二次根式的定义可知b2+2b+2=3+2b,从而可求得b的值.
解答 解:∵最简二次根式$\sqrt{{b}^{2}+2b+2}$与$\sqrt{3+2b}$是同类根式,
∴b2+2b+2=3+2b.
整理得:b2=1.
解得:b1=1,b2=-1.
当b=-1时,$\sqrt{{b}^{2}+2b+2}$=1,$\sqrt{3+2b}$=1不合题意.
故答案为;1.
点评 本题主要考查的是同类二次根式的定义,掌握同类二次根式的定义是解题的关键.

练习册系列答案
相关题目
4.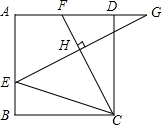 如图,在边长为3的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG=1,连接EG,CF⊥EG交EG于点H,交AD于点F,则$\frac{FH}{CH}$=( )
如图,在边长为3的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG=1,连接EG,CF⊥EG交EG于点H,交AD于点F,则$\frac{FH}{CH}$=( )
 如图,在边长为3的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG=1,连接EG,CF⊥EG交EG于点H,交AD于点F,则$\frac{FH}{CH}$=( )
如图,在边长为3的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG=1,连接EG,CF⊥EG交EG于点H,交AD于点F,则$\frac{FH}{CH}$=( )| A. | 1:1 | B. | 1:$\sqrt{2}$ | C. | 1:$\sqrt{3}$ | D. | 1:2 |
18.下列图形中,∠1与∠2是内错角的是( )
| A. |  | B. | 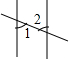 | C. | 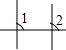 | D. | 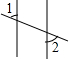 |
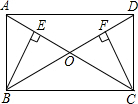 如图,矩形ABCD中,AC与BD交于O点,BE⊥AC于E,CF⊥BD于F.
如图,矩形ABCD中,AC与BD交于O点,BE⊥AC于E,CF⊥BD于F. 如图,菱形ABCD的边长为4cm,且∠ABC=120°,E是BC的中点,在BD上求点P,使PC+PE取最小值,并求这个最小值.
如图,菱形ABCD的边长为4cm,且∠ABC=120°,E是BC的中点,在BD上求点P,使PC+PE取最小值,并求这个最小值.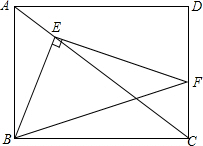 如图所示,矩形ABCD的边AB=3,Rt△BEF的直角顶点E在对角线AC上,另一顶点F在边CD上,若△BEF的一个锐角为30°,则BC的长为3$\sqrt{3}$或$\sqrt{3}$.
如图所示,矩形ABCD的边AB=3,Rt△BEF的直角顶点E在对角线AC上,另一顶点F在边CD上,若△BEF的一个锐角为30°,则BC的长为3$\sqrt{3}$或$\sqrt{3}$.