题目内容
3.随着我国汽车产业的发展,城市道路拥堵问题日益严峻.某部门对15个城市的交通状况进行了调查,得到的数据如表所示:| 城市 项目 | 北京 | 太原 | 杭州 | 沈阳 | 广州 | 深圳 | 上海 | 桂林 | 南遇 | 海口 | 南京 | 温州 | 威海 | 兰州 | 中山 |
| 上班花费时间(分钟) | 52 | 33 | 34 | 34 | 48 | 45 | 47 | 23 | 24 | 24 | 37 | 25 | 24 | 25 | 18 |
| 上班堵车时间(分钟) | 14 | 12 | 12 | 12 | 12 | 11 | 11 | 7 | 7 | 6 | 6 | 5 | 5 | 5 | 0 |
(2)求15个城市的平均上班堵车时间(计算结果保留一位小数);
(3)规定:城市堵车率=$\frac{上班堵车时间}{上班花费时间-上班堵车时间}$×100%,比如:北京的堵车率=$\frac{14}{52-14}$×100%=36.8%;沈阳的堵车率=$\frac{12}{34-12}$×100%=54.4%.某人欲从北京、沈阳、上海、温州四个城市中任意选取两个作为出发目的地,求选取的两个城市的堵车率超过30%的概率.
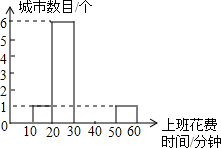
分析 (1)从统计表中找出上班花费时间在30~40和40~50分钟的城市个数,然后补全频数统计图;
(2)根据加权平均数的定义计算;
(3)先计算出上海的堵车率和温州的堵车率,再画树状图展示所有12种等可能的结果数,然后找出两个城市的堵车率超过30%的结果数,再根据概率公式计算.
解答 解:(1)如图,
(2)15个城市的平均上班堵车时间=(14+12×4+11×2+7×2+6×2+5×3+0)≈8.3(分钟);
(3)上海的堵车率=$\frac{11}{47-11}$×100%=30.6%;温州的堵车率=$\frac{5}{25-5}$×100%=25%.
画树状图为:
共有12种等可能的结果数,其中两个城市的堵车率超过30%的结果数为6,
所以两个城市的堵车率超过30%的概率=$\frac{6}{12}$=$\frac{1}{2}$.
点评 本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.也考查了统计图.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
15.反比例函数y=$\frac{-2}{x}$的图象上点A(2,m)到原点的距离AO等于( )
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | 3 | D. | 2$\sqrt{2}$ |
12.若点P是y轴上一动点,则点P到点A(-2,5)和B(-4,3)的距离之和最短时,点P的坐标为( )
| A. | (0,$\frac{8}{3}$) | B. | (0,-$\frac{8}{3}$) | C. | (0,$\frac{13}{3}$) | D. | (0,-$\frac{13}{3}$) |
13.下列四个实数中,无理数是( )
| A. | 1.732 | B. | $\frac{22}{7}$ | C. | $\sqrt{8}$ | D. | 1.$\stackrel{•}{3}$ |
 在平面直角坐标系中描出点A(-2,0)、B(3,1)、C(2,3),将各点用线段依次连接起来,并解答如下问题:
在平面直角坐标系中描出点A(-2,0)、B(3,1)、C(2,3),将各点用线段依次连接起来,并解答如下问题: