题目内容
12.若点P是y轴上一动点,则点P到点A(-2,5)和B(-4,3)的距离之和最短时,点P的坐标为( )| A. | (0,$\frac{8}{3}$) | B. | (0,-$\frac{8}{3}$) | C. | (0,$\frac{13}{3}$) | D. | (0,-$\frac{13}{3}$) |
分析 首先作点A关于y轴的对称点C连接CB,CB与y轴交点即为P点,先求出过C,B两点的直线函数关系式,再求出直线与y轴交点P点坐标即可.
解答 解:点A关于y轴的对称点的坐标C((2,5),连接BC与Y轴的交点为P,
此时PA+PB最小,设直线BC为y=kx+b由题意:$\left\{\begin{array}{l}{-4k+b=3}\\{2k+b=5}\end{array}\right.$解得$\left\{\begin{array}{l}{k=\frac{1}{3}}\\{b=\frac{13}{3}}\end{array}\right.$,
∴直线BC为y=$\frac{1}{3}x$+$\frac{13}{3}$,
∴点P(0,$\frac{13}{3}$).
故选C.
点评 此题主要考查了求一次函数关系式,以及轴对称求最短路线,关键是作出点A关于y轴的对称点C,求出过C,B两点的直线函数关系式,属于中考常考题型.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
3.随着我国汽车产业的发展,城市道路拥堵问题日益严峻.某部门对15个城市的交通状况进行了调查,得到的数据如表所示:
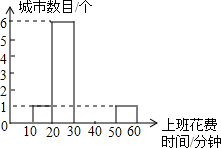
(1)根据上班花费时间,将下面的频数分布直方图补充完整;
(2)求15个城市的平均上班堵车时间(计算结果保留一位小数);
(3)规定:城市堵车率=$\frac{上班堵车时间}{上班花费时间-上班堵车时间}$×100%,比如:北京的堵车率=$\frac{14}{52-14}$×100%=36.8%;沈阳的堵车率=$\frac{12}{34-12}$×100%=54.4%.某人欲从北京、沈阳、上海、温州四个城市中任意选取两个作为出发目的地,求选取的两个城市的堵车率超过30%的概率.
| 城市 项目 | 北京 | 太原 | 杭州 | 沈阳 | 广州 | 深圳 | 上海 | 桂林 | 南遇 | 海口 | 南京 | 温州 | 威海 | 兰州 | 中山 |
| 上班花费时间(分钟) | 52 | 33 | 34 | 34 | 48 | 45 | 47 | 23 | 24 | 24 | 37 | 25 | 24 | 25 | 18 |
| 上班堵车时间(分钟) | 14 | 12 | 12 | 12 | 12 | 11 | 11 | 7 | 7 | 6 | 6 | 5 | 5 | 5 | 0 |
(2)求15个城市的平均上班堵车时间(计算结果保留一位小数);
(3)规定:城市堵车率=$\frac{上班堵车时间}{上班花费时间-上班堵车时间}$×100%,比如:北京的堵车率=$\frac{14}{52-14}$×100%=36.8%;沈阳的堵车率=$\frac{12}{34-12}$×100%=54.4%.某人欲从北京、沈阳、上海、温州四个城市中任意选取两个作为出发目的地,求选取的两个城市的堵车率超过30%的概率.

4.已知一个圆锥形零件的高线为$\sqrt{5}$,底面圆半径为2,则它的侧面积为( )
| A. | 2$\sqrt{5}$ | B. | 2π | C. | 6π | D. | 3$\sqrt{5}$π |
2. 如图,Rt△ABC中,∠ACB=90°,∠A=35°,D是AB上一点,将△ABC沿CD折叠,使B点落在AC边上的处,则∠ADB1等于( )
如图,Rt△ABC中,∠ACB=90°,∠A=35°,D是AB上一点,将△ABC沿CD折叠,使B点落在AC边上的处,则∠ADB1等于( )
 如图,Rt△ABC中,∠ACB=90°,∠A=35°,D是AB上一点,将△ABC沿CD折叠,使B点落在AC边上的处,则∠ADB1等于( )
如图,Rt△ABC中,∠ACB=90°,∠A=35°,D是AB上一点,将△ABC沿CD折叠,使B点落在AC边上的处,则∠ADB1等于( )| A. | 10° | B. | 15° | C. | 20° | D. | 30° |
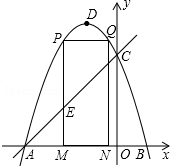 如图,抛物线y=-x2-2x+3 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
如图,抛物线y=-x2-2x+3 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.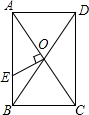 如图,矩形ABCD的对角线AC,BD相交于点O,过点O作OE⊥AC交AB于E,若BC=4,△AOE的面积为5,则AE=5.
如图,矩形ABCD的对角线AC,BD相交于点O,过点O作OE⊥AC交AB于E,若BC=4,△AOE的面积为5,则AE=5. 如图,直角三角形ABC中,∠ACB=90°,AB=15,BC=9,在线段AB上取一点D,作DF⊥AB交AC于点F.现将△ADF沿DF折叠,使点A落在线段DB上,对应点记为A1;AD的中点E的对应点记为E1,若△E1FA1∽△E1BF,求AD的长.
如图,直角三角形ABC中,∠ACB=90°,AB=15,BC=9,在线段AB上取一点D,作DF⊥AB交AC于点F.现将△ADF沿DF折叠,使点A落在线段DB上,对应点记为A1;AD的中点E的对应点记为E1,若△E1FA1∽△E1BF,求AD的长.